题目内容
19.已知x,y满足(x-1)2+y2=1,则2x+y的最大值为$\sqrt{5}$+2.分析 令x-2=cosθ,y=sinθ,则2x+y=2(cosθ+1)+sinθ=2cosθ+sinθ+2=$\sqrt{5}$cos(θ+φ)+2,进而得到答案.
解答 解:∵(x-1)2+y2=1,
∴可令x-1=cosθ,y=sinθ,
∴2x+y=2(cosθ+1)+sinθ=2cosθ+sinθ+2=$\sqrt{5}$cos(θ+φ)+2,
故2x+y的最大值为$\sqrt{5}$+2,
故答案为:$\sqrt{5}$+2.
点评 本题考查的知识点是三角函数的最大值,转化思想,圆的参数方程,难度中档.

练习册系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{f(x-1)+1,x>0}\end{array}\right.$当x∈[0,10]时,关于x的方程f(x)=x的所有解的和为( )
| A. | 50 | B. | 55 | C. | 60 | D. | 65 |
14.尘肺病是一种严重的职业病,新密市职工张海超“开胸验肺”的举动引起了社会的极大关注.据悉尘肺病的产生,与工人长期生活在粉尘环境有直接的关系.下面是一项调查数据:
请由此分析我们有多大的把握认为是否患有尘肺病与是否有过粉尘环境工作经历有关系.
| 有过粉尘环境工作经历 | 无粉尘环境工作经历 | 合计 | |
| 有尘肺病 | 22 | 2 | 24 |
| 无尘肺病 | 898 | 1498 | 2396 |
| 合计 | 920 | 1500 | 2420 |
4.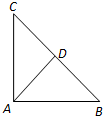 如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )
如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )
 如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )
如图,已知△ABC中,AB=AC=4,∠BAC=$\frac{π}{2}$,点D是BC的中点,若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$,且点M在△ACD的内部(不含边界),则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是( )| A. | (-2,4) | B. | (-2,6) | C. | (0,4) | D. | (0,6) |
9.已知函数f(x)满足f(0)=0,且在[0,+∞)上单调递增,若f(lg x)>0,则x的取值范围是( )
| A. | (0,1) | B. | (1,10) | C. | (1,+∞) | D. | (10,+∞) |