题目内容
8．已知正实数x，y满足$\frac{1}{x}$+$\frac{2}{y}$=1，那么2x+3y的最小值为8+4$\sqrt{3}$．分析 根据正实数x，y满足$\frac{1}{x}$+$\frac{2}{y}$=1，将2x+3y转化成（2x+3y）（$\frac{1}{x}$+$\frac{2}{y}$），然后利用基本不等式可求出最值，注意等号成立的条件．
解答 解：∵正实数x，y满足$\frac{1}{x}$+$\frac{2}{y}$=1，
∴2x+3y=（2x+3y）（$\frac{1}{x}$+$\frac{2}{y}$）=2+6+$\frac{3y}{x}$+$\frac{4x}{y}$≥8+4$\sqrt{3}$，
当且仅当$\frac{3y}{x}$=$\frac{4x}{y}$时取等号
∴2x+3y的最小值为8+4$\sqrt{3}$．
故答案为：8+4$\sqrt{3}$．
点评 本题主要考查了基本不等式的应用，注意检验等号成立的条件，式子的变形是解题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
3．某食品安检部门调查一个养殖场的养殖鱼的有关情况，安检人员从这个养殖场中不同位置共捕捞出100条鱼，称得每条鱼的重量（单位：千克），并将所得数据进行统计得如表．
若规定重量大于或等于1.20kg的鱼占捕捞鱼总量的15%以上时，则认为所饲养的鱼有问题，否则认为所饲养的鱼没有问题．
（1）根据统计表，估计数据落在[1.20，1.30）中的概率约为多少，并判断此养殖场所饲养的鱼是否有问题？
（2）上面所捕捞的100条鱼中，从重量在[1.00，1.05）和[1.25，1.30）的鱼中，任取2条鱼来检测，求恰好所取得鱼的重量在[1.00，1.05）和[1，.25，1.30）中各有1条的概率．
| 鱼的重量 | [1.00，1.05） | [1.05，1.10） | [1.10，1.15） | [1.15，1.20） | [1.20，1.25） | [1.25，1.30） |
| 鱼的条数 | 3 | 20 | 35 | 31 | 9 | 2 |
（1）根据统计表，估计数据落在[1.20，1.30）中的概率约为多少，并判断此养殖场所饲养的鱼是否有问题？
（2）上面所捕捞的100条鱼中，从重量在[1.00，1.05）和[1.25，1.30）的鱼中，任取2条鱼来检测，求恰好所取得鱼的重量在[1.00，1.05）和[1，.25，1.30）中各有1条的概率．
20．函数y=x2-2lnx的单调递减区间是（ ）
| A． | （-∞，-1]∪（0，1] | B． | [-1，0）∪（0，1] | C． | [1，+∞） | D． | （0，1] |
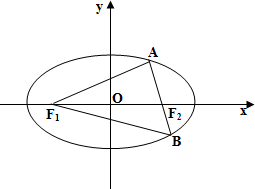设椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的一个焦点与抛物线y2=4x的焦点重合，离心率e=$\frac{1}{2}$，F1，F2分别为左、右焦点，AB是过右焦点的弦．