题目内容
9.已知函数f(x)满足f(0)=0,且在[0,+∞)上单调递增,若f(lg x)>0,则x的取值范围是( )| A. | (0,1) | B. | (1,10) | C. | (1,+∞) | D. | (10,+∞) |
分析 根据函数题意,得出f(lg x)>0时lgx>0,从而求得x的取值范围.
解答 解:∵函数f(x)满足f(0)=0,且在[0,+∞)上单调递增,
∴当f(lg x)>0时,lgx>0,
解得x>1;
∴x的取值范围是(1,+∞).
故选:C.
点评 本题考查了函数的单调性质的应用问题,也考查了对数函数的性质与应用问题,是基础题目.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
20.函数y=x2-2lnx的单调递减区间是( )
| A. | (-∞,-1]∪(0,1] | B. | [-1,0)∪(0,1] | C. | [1,+∞) | D. | (0,1] |
14.已知随机变量X~N(0,σ2),且P(X>2)=0.4,则P(-2≤X≤0)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
19.已知函数y=Asin(ωx+φ)(A>0,ω>0)的最大值为4,最小值为-4,最小正周期为$\frac{π}{2}$,直线x=$\frac{π}{3}$是其图象的一条对称轴,则符合条件的函数解析式是( )
| A. | y=4sin(4x+$\frac{π}{6}$) | B. | y=4sin(4x+$\frac{π}{3}$) | C. | y=2sin(4x+$\frac{π}{3}$) | D. | y=2sin(4x+$\frac{π}{6}$) |
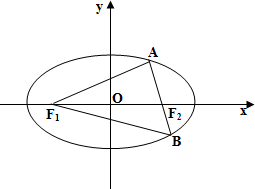 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.