题目内容
11.已知四边形MNPQ的顶点M(1,1),N(3,-1),P(4,0),Q(2,2),(1)求斜率kMN与斜率kPQ;
(2)求证:四边形MNPQ为矩形.
分析 (1)利用向量公式求解即可.
(2)判断直线是否平行与垂直,推出结果.
解答 解:(1)四边形MNPQ的顶点M(1,1),N(3,-1),P(4,0),Q(2,2),
斜率kMN=$\frac{-1-1}{3-1}$=-1
斜率kPQ=$\frac{2-0}{2-4}$=-1.
(2)证明:由(1)可知:kMN=kPQ;
即有MN∥PQ,
斜率 kMQ=$\frac{2-1}{2-1}$=1
斜率kPN=$\frac{0+1}{4-3}$=1.
可知PN∥MQ,
并且PQ⊥PN,
所以,四边形MNPQ为矩形.
点评 本题考查直线的斜率与直线与直线的平行与垂直关系的判断,是基础题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
3.某食品安检部门调查一个养殖场的养殖鱼的有关情况,安检人员从这个养殖场中不同位置共捕捞出100条鱼,称得每条鱼的重量(单位:千克),并将所得数据进行统计得如表.
若规定重量大于或等于1.20kg的鱼占捕捞鱼总量的15%以上时,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
(1)根据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否有问题?
(2)上面所捕捞的100条鱼中,从重量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得鱼的重量在[1.00,1.05)和[1,.25,1.30)中各有1条的概率.
| 鱼的重量 | [1.00,1.05) | [1.05,1.10) | [1.10,1.15) | [1.15,1.20) | [1.20,1.25) | [1.25,1.30) |
| 鱼的条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(1)根据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否有问题?
(2)上面所捕捞的100条鱼中,从重量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得鱼的重量在[1.00,1.05)和[1,.25,1.30)中各有1条的概率.
20.函数y=x2-2lnx的单调递减区间是( )
| A. | (-∞,-1]∪(0,1] | B. | [-1,0)∪(0,1] | C. | [1,+∞) | D. | (0,1] |
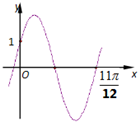 已知函数f(x)=2sin(ωx+ϕ)(ω>0,|ϕ|<$\frac{π}{2}$)的图象如图所示,则函数f(x)的解析式是f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=2sin(ωx+ϕ)(ω>0,|ϕ|<$\frac{π}{2}$)的图象如图所示,则函数f(x)的解析式是f(x)=2sin(2x+$\frac{π}{6}$).