题目内容
已知函数f(x)=ex+1-x-2.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若x≥-1时,不等式f(x)≥
(x+1)2恒成立,求实数a的取值范围.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若x≥-1时,不等式f(x)≥
| a |
| 2 |
考点:利用导数研究函数的单调性,函数恒成立问题
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,根据函数单调性和导数之间的关系即可得到结论.
(Ⅱ)将不等式f(x)≤x2恒成立进行转化为求函数的最值问题,利用导数结合分类讨论即可求a的取值范围.
(Ⅱ)将不等式f(x)≤x2恒成立进行转化为求函数的最值问题,利用导数结合分类讨论即可求a的取值范围.
解答:
解:(Ⅰ)∵f(x)=ex+1-x-2,
∴f′(x)=ex+1-1,可得f′(x)=0的根为x=-1
当x<-1时,f′(x)<0,可得函数在区间(-∞,-1)上为减函数;
当x>-1时,f′(x)>0,可得函数在区间(-1,+∞)上为增函数.
(Ⅱ)∵函数f(x)在区间[-1,+∞)上为增函数,
∴f(x)≥f(-1)=0,
若a≤0,则
(x+1)2≤0≤f(x)成立,此时满足条件.
若a>0,令g(x)=f(x)-
(x+1)2,
则g′(x)=ex+1-a(x+1)=h(x),
则h′(x)=ex+1-a,
当x≥-1时,ex+1≥1,
当0<a≤1时,h′(x)≥0,此时h(x)在区间[-1,+∞)上为增函数.
∴h(x)≥h(-1)=0,即g′(x)>0,∴g(x)的最小值为g(-1)=0.
当a>1时,令h′(x)=0,解得x=lna-1>-1,
当x∈(-1,lna-1)时,h′(x)<0,此时函数单调递减.
∴h(x)<h(-1)<0,
即g′(x)<0,g(x)在(-1,lna-1)递减,∴g(lna-1)<g(-1)=0,
此时g(x)≥0不恒成立,
综上实数a的取值范围是(-∞,1].
∴f′(x)=ex+1-1,可得f′(x)=0的根为x=-1
当x<-1时,f′(x)<0,可得函数在区间(-∞,-1)上为减函数;
当x>-1时,f′(x)>0,可得函数在区间(-1,+∞)上为增函数.
(Ⅱ)∵函数f(x)在区间[-1,+∞)上为增函数,
∴f(x)≥f(-1)=0,
若a≤0,则
| a |
| 2 |
若a>0,令g(x)=f(x)-
| a |
| 2 |
则g′(x)=ex+1-a(x+1)=h(x),
则h′(x)=ex+1-a,
当x≥-1时,ex+1≥1,
当0<a≤1时,h′(x)≥0,此时h(x)在区间[-1,+∞)上为增函数.
∴h(x)≥h(-1)=0,即g′(x)>0,∴g(x)的最小值为g(-1)=0.
当a>1时,令h′(x)=0,解得x=lna-1>-1,
当x∈(-1,lna-1)时,h′(x)<0,此时函数单调递减.
∴h(x)<h(-1)<0,
即g′(x)<0,g(x)在(-1,lna-1)递减,∴g(lna-1)<g(-1)=0,
此时g(x)≥0不恒成立,
综上实数a的取值范围是(-∞,1].
点评:本题主要考查函数单调性和导数之间的关系和应用,以及利用函数的导数研究函数恒成立问题,综合性较强,运算量较大.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
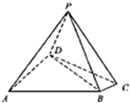 如图,四棱锥P-ABCD,∠DAB=90°,BC⊥CD,∠CDB=30°,且PA=PB=PD=AB=AD=
如图,四棱锥P-ABCD,∠DAB=90°,BC⊥CD,∠CDB=30°,且PA=PB=PD=AB=AD= 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,点E为PA中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,点E为PA中点.