题目内容
已知函数f(x)=2ax-
,x∈(0,1],求f(x)在区间(0,1]上的最大值.
| 1 |
| x2 |
考点:函数的最值及其几何意义
专题:综合题,导数的综合应用
分析:求导数,分类讨论,确定函数的单调性,即可求f(x)在区间(0,1]上的最大值.
解答:
解:∵函数f(x)=2ax-
,∴f′(x)=2a+
当a≥-1时,f(x)在(0,1]上为增函数,∴[f(x)]max=f(1)=2a-1.
当a<-1时,令f′(x)=0得x=
∵0<
<1,∴0<x<
时,f′(x)>0;
<x≤1时,f′(x)<0.∴f(x)在(0,
)上是增函数,在(
,1]减函数.
∴[f(x)]max=f(
)=-3
.
| 1 |
| x2 |
| 2 |
| x3 |
当a≥-1时,f(x)在(0,1]上为增函数,∴[f(x)]max=f(1)=2a-1.
当a<-1时,令f′(x)=0得x=
| 1 | |||
|
∵0<
| 1 | |||
|
| 1 | |||
|
| 1 | |||
|
| 1 | |||
|
| 1 | |||
|
∴[f(x)]max=f(
| 1 | |||
|
| 3 | a2 |
点评:本题考查函数的最值及其几何意义,考查函数的单调性,正确分类是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
求
的值( )
| 4 | (3-π)4 |
| A、0 | B、3-π | C、π-3 | D、无解 |
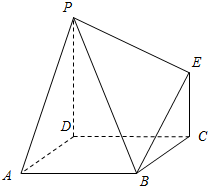 如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.