题目内容
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.如:6=1+2+3;28=1+2+4+7+14;496=1+2+4+8+16+31+62+124+248.已经证明:若2n-1是质数,则2n-1(2n-1)是完全数,n∈N*.请写出一个四位完全数 ;又6=2×3,所以6的所有正约数之和可表示为(1+2)•(1+3);28=22×7,所以28的所有正约数之和可表示为(1+2+22)•(1+7);按此规律,请写出所给的四位数的所有正约数之和可表示为 .(请参照6与28的形式给出)
考点:进行简单的合情推理
专题:空间位置关系与距离
分析:根据已知中若2n-1是质数,则2n-1(2n-1)是完全数,令n=7可得一个四位完全数,进而根据已知中6的所有正约数之和及28的所有正约数之和的表达形式得到8128的所有正约数之和.
解答:
解:若2n-1是质数,则2n-1(2n-1)是完全数,
令n=7可得一个四位完全数为64×127=8128.
由题意可令8128=26×(27-1)=26×127,
其所有正约数之和为(1+2+22+23+24+25+26)•(1+127),
故答案为:8128,(1+2+22+23+24+25+26)•(1+127)
令n=7可得一个四位完全数为64×127=8128.
由题意可令8128=26×(27-1)=26×127,
其所有正约数之和为(1+2+22+23+24+25+26)•(1+127),
故答案为:8128,(1+2+22+23+24+25+26)•(1+127)
点评:本题考查合情推理,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
设正六边形ABCDEF的中心为点O,P为平面内任意一点,则
+
+
+
+
+
=( )
| PA |
| PB |
| PC |
| PD |
| PE |
| PF |
A、
| ||
B、
| ||
C、3
| ||
D、6
|
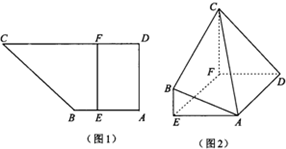 如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.
如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2. 如图,AB是⊙O的直径,PB,PC分别切⊙O于B,C,若∠ACE=38°,则∠P=
如图,AB是⊙O的直径,PB,PC分别切⊙O于B,C,若∠ACE=38°,则∠P=