题目内容
已知各项均为正数的数列{an}满足an+12-an+1an-2an2=0,n∈N﹡,且a3+2是a2,a4的等差中项.数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
an-
bn,求数列{cn}的前2n项和T2n.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
| 1-(-1)n |
| 2 |
| 1+(-1)n |
| 2 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件推导出数列{an}是以2为公比的等比数列,由此求出数列{an}的通项公式an=2n.{bn}是首项为1,公差为2的等差数列,由此求出bn=2n-1.
(2)cn=
,由此利用分组求和法能求出数列{cn}的前2n项和T2n.
(2)cn=
|
解答:
解:(1)∵an+12-an+1an-2an2=0,∴(an+1+an)(an+1-2an)=0,
∵数列{an}的各项均为正数,
∴an+1+an>0,
∴an+1-2an=0,
即an+1=2an,所以数列{an}是以2为公比的等比数列.
∵a3+2是a2,a4的等差中项,
∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,
∴a1=2,
∴数列{an}的通项公式an=2n.
∵数列{bn}满足b1=1,且bn+1=bn+2.
∴{bn}是首项为1,公差为2的等差数列,
∴bn=1+(n-1)×2=2n-1.…(6分)
(2)∵cn=
an-
bn
=
•2n-
•(2n-1)
=
,
∴T2n=(2+23+…+2n-1)-[(3+7+…+(4n-1)]
=
-
=
-2n2-n.…(12分)
∵数列{an}的各项均为正数,
∴an+1+an>0,
∴an+1-2an=0,
即an+1=2an,所以数列{an}是以2为公比的等比数列.
∵a3+2是a2,a4的等差中项,
∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,
∴a1=2,
∴数列{an}的通项公式an=2n.
∵数列{bn}满足b1=1,且bn+1=bn+2.
∴{bn}是首项为1,公差为2的等差数列,
∴bn=1+(n-1)×2=2n-1.…(6分)
(2)∵cn=
| 1-(-1)n |
| 2 |
| 1+(-1)n |
| 2 |
=
| 1-(-1)n |
| 2 |
| 1+(-1)n |
| 2 |
=
|
∴T2n=(2+23+…+2n-1)-[(3+7+…+(4n-1)]
=
| 2(1-4n) |
| 1-4 |
| n(3+4n-1) |
| 2 |
=
| 22n+1-2 |
| 3 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
相关题目
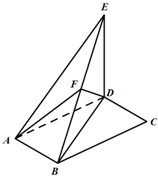 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.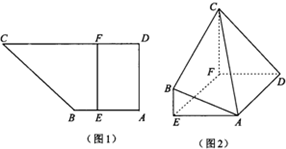 如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.
如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.