题目内容
15．不等式x2-|x|-2＜0（x∈R）的解集是（ ）| A． | {x|x＜-1或x＞1} | B． | {x|x＜-2或x＞2} | C． | {x|-1＜x＜1} | D． | {x|-2＜x＜2} |
分析 把原不等式中的x2变为|x|2，则不等式变为关于|x|的一元二次不等式，求出解集得到关于x的绝对值不等式，解出绝对值不等式即可得到x的解集．
解答 解：原不等式化为|x|2-|x|-2＜0
因式分解得（|x|-2）（|x|+1）＜0
因为|x|+1＞0，所以|x|-2＜0即|x|＜2
解得：-2＜x＜2．
故选D．
点评 本题考查一元二次不等式的解法，解题的突破点是把原不等式中的x2变为|x|2，是一道中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
3．△ABC中，$tanA=\frac{3}{4}$，则cos2A等于（ ）
| A． | $\frac{18}{25}$ | B． | $-\frac{18}{25}$ | C． | $-\frac{7}{25}$ | D． | $\frac{7}{25}$ |
20．已知集合A={-2，-1，0，1，2}，B={x|（x+1）（x-2）＜0}，则A∩B=（ ）
| A． | {0，1} | B． | {-1，0} | C． | {-1，0，1} | D． | {0，1，2} |
5．下列方格纸中每个正方形的边长为1，粗线部分是一个几何体的三视图，则该几何体最长棱的棱长是（ ）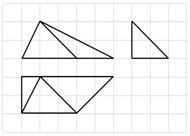
| A． | 3 | B． | 6 | C． | $2\sqrt{5}$ | D． | 5 |