题目内容
13.已知一个几何体的三视图如图所示,则该几何体的体积为( )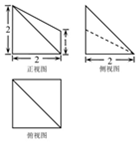
| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{13}{3}$ | D. | 5 |
分析 根据几何体的三视图知,该几何体是四棱锥与三棱锥的组合体,
画出图形,结合图形求出它的体积.
解答 解:根据几何体的三视图知,
该几何体是四棱锥与三棱锥的组合体,如图所示;
结合图中数据,计算它的体积为
V=V四棱锥P-ABCD+V三棱锥P-CDM
=$\frac{1}{3}$×22×2+$\frac{1}{3}$×$\frac{1}{2}$×2×1×2
=$\frac{10}{3}$.
故选:A.
点评 本题考查了几何体三视图的应用问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.△ABC中,$tanA=\frac{3}{4}$,则cos2A等于( )
| A. | $\frac{18}{25}$ | B. | $-\frac{18}{25}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |
5.下列方格纸中每个正方形的边长为1,粗线部分是一个几何体的三视图,则该几何体最长棱的棱长是( )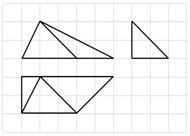

| A. | 3 | B. | 6 | C. | $2\sqrt{5}$ | D. | 5 |
3.下列可以用来分析身高和体重之间的关系的是( )
| A. | 残差分析 | B. | 回归分析 | C. | 等高条形图 | D. | 独立性检验 |
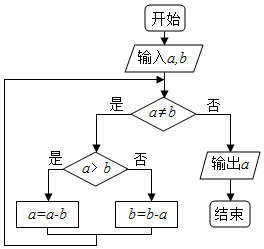 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )