题目内容
16.已知点A为抛物线C:x2=4y上的动点(不含原点),过点A的切线交x轴于点B,设抛物线C的焦点为F,则∠ABF一定是直角.(填:钝角、锐角、直角)分析 求导数,利用点斜式方程求得过A的切线方程,解出B的坐标,求出$\overrightarrow{BA}$,$\overrightarrow{BF}$的坐标,可得计算$\overrightarrow{BA}$•$\overrightarrow{BF}$=0即可得出结论.
解答 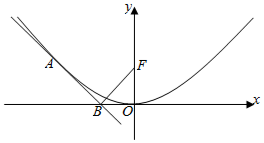 解:由x2=4y可得y=$\frac{1}{4}$x2,求导y′=$\frac{1}{2}$x,
解:由x2=4y可得y=$\frac{1}{4}$x2,求导y′=$\frac{1}{2}$x,
设A(x0,$\frac{{x}_{0}^{2}}{4}$),则
过A的切线方程为y-$\frac{{x}_{0}^{2}}{4}$=$\frac{1}{2}$x0(x-x0),
令y=0,可得x=$\frac{1}{2}$x0,则B($\frac{1}{2}$x0,0),
∵F(0,1),
∴$\overrightarrow{BA}$=($\frac{1}{2}$x0,$\frac{{x}_{0}^{2}}{4}$),$\overrightarrow{BF}$=(-$\frac{1}{2}$x0,1),
∴$\overrightarrow{BA}$•$\overrightarrow{BF}$=0,
∴∠ABF=90°,
∠ABF一定是直角,
故答案为:直角.
点评 本题考查直线与抛物线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
11.已知$f(x)=sin\frac{πx}{6}(x∈R)$,则f(1)+f(2)+f(3)+…+f(2017)=( )
| A. | 2017 | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
5.下列方格纸中每个正方形的边长为1,粗线部分是一个几何体的三视图,则该几何体最长棱的棱长是( )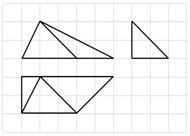

| A. | 3 | B. | 6 | C. | $2\sqrt{5}$ | D. | 5 |