题目内容

17．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（　　）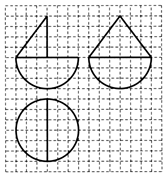
A．24πB．30πC．42πD．60π

分析 由三视图可得，直观图为半球与半棱锥的组合体，即可求出几何体的体积．

解答 解：由三视图可得，直观图为半球与半棱锥的组合体，体积为$\frac{1}{2}×\frac{4}{3}π×{3}^{3}+\frac{1}{2}×\frac{1}{3}×π×{3}^{2}×4$=24π，
故选：A．

点评 本题考查了体积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
7．已知函数f（x）=$\frac{1}{a}$-$\frac{1}{x}$ （a＞0，x＞0）．
（1）用定义法证明：f（x）在（0，+∞）上是增函数；
（2）若f（x）≤2x在（0，+∞）上恒成立，求a的取值范围；
（3）若f（x）在[m，n]上的值域是[m，n]（m≠n），求a的取值范围．
8．已知P1（2，-1），P2（0，5），且点P在线段P1P2的延长线上，且$|\overrightarrow{{P_1}{P_2}}|=2|\overrightarrow{P{P_2}}|$，则点P的坐标是（-1，8）．
5．下列方格纸中每个正方形的边长为1，粗线部分是一个几何体的三视图，则该几何体最长棱的棱长是（　　）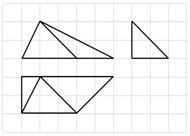
A．3B．6C．$2\sqrt{5}$D．5
12．下列命题中的真命题是（　　）
A．?x∈R使得sinx+cosx=1.5B．?x∈（0，π），sinx＞cosx
C．?x∈R使得x2+x=-1D．?x∈（0，+∞），ex＞x+1
2．等差数列{an}的前n项和为Sn，且a1=1，a4=7，则S10=100．
9．已知f（x）=$\left\{\begin{array}{l}{cosπx，（x＜1）}\\{f（x-1），（x≥1）}\end{array}\right.$，求$f（{\frac{1}{3}}）+f（{\frac{4}{3}}）$的值（　　）
A．0B．$\frac{1}{2}$C．1D．$\frac{3}{2}$
6．命题“$?{x_0}∈R，使得x_0^2≥0$”的命题的否定为?x∈R，使得x2＜0．
7．执行如图所示的程序框图，如果输出的$S=\frac{7}{15}$，则输入的n（　　）
A．6B．7C．8D．9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网