题目内容
函数f(x)=(1+x-
+
-
+…-
+
)•sin2x在区间[-3,3]上的零点的个数为( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
| A、3 | B、4 | C、5 | D、6 |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:由题意化求函数f(x)=(1+x-
+
-
+…-
+
)•sin2x在区间[-3,3]上的零点的个数为g(x)=1+x-
+
-
+…-
+
的零点个数与sin2x在[-3,3]上的零点个数,从而求解.
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
解答:
解:令g(x)=1+x-
+
-
+…-
+
,
g′(x)=1-x+x2-x3+…+x2012,
当x=0时,g′(0)=1>0;
当x=-1时,g′(-1)=2013>0;
当x≠0且x≠-1时,
g′(x)=
=
>0;
故g(x)=1+x-
+
-
+…-
+
在R上是增函数,
又∵g(-1)=1-1-
-
-
…-
<0;
g(0)=1>0;
故g(x)=1+x-
+
-
+…-
+
在(-1,0)上有零点,
而sin2x在[-3,3]上的零点为0,±
;
故函数f(x)=(1+x-
+
-
+…-
+
)•sin2x在区间[-3,3]上的零点的个数为4;
故选B.
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
g′(x)=1-x+x2-x3+…+x2012,
当x=0时,g′(0)=1>0;
当x=-1时,g′(-1)=2013>0;
当x≠0且x≠-1时,
g′(x)=
| 1-(-x)2013 |
| 1+x |
| 1+x2013 |
| 1+x |
故g(x)=1+x-
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
又∵g(-1)=1-1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2013 |
g(0)=1>0;
故g(x)=1+x-
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
而sin2x在[-3,3]上的零点为0,±
| π |
| 2 |
故函数f(x)=(1+x-
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2012 |
| 2012 |
| x2013 |
| 2013 |
故选B.
点评:本题考查了函数的零点的个数的判断,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
设学生的考试成绩为G,则下面的代码的算法目的是( )


| A、计算50个学生的平均成绩 |
| B、计算50个学生中不及格的人数 |
| C、计算50个学生中及格的人数 |
| D、计算50个学生的总成绩 |
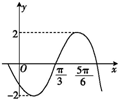 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )A、f(x)=2sin(
| ||||
B、f(x)=2sin(x-
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(2x-
|
若函数f(x)=
是R上的增函数,则实数a的取值范围为( )
|
| A、(1,+∞) |
| B、(1,8) |
| C、[4,8) |
| D、(4,8) |