题目内容
下列有关命题的叙述错误的是( )
| A、对于命题P:?x∈R,x2+x-1<0,则¬P为:?x∈R,x2+x-1≥0 |
| B、若“P且Q”为假命题,则P,Q均为假命题 |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
考点:命题的真假判断与应用
专题:简易逻辑
分析:通过命题的否定判断A的正误;利用复合命题的真假判断B的正误;利用充要条件判断C的正误;四种命题的逆否关系判断D的正误.
解答:
解:对于A,满足全称命题与特称命题的否定关系,所以A正确;
对于B,若“P且Q”为假命题,则P,Q一个是假命题就是假命题.不一定均为假命题,所以B不正确;
对于C,“x>2”可得“x2-3x+2>0”,所以“x>2”是“x2-3x+2>0”的充分不必要条件,是C正确;
对于D,命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,满足逆否命题的关系.
故选B.
对于B,若“P且Q”为假命题,则P,Q一个是假命题就是假命题.不一定均为假命题,所以B不正确;
对于C,“x>2”可得“x2-3x+2>0”,所以“x>2”是“x2-3x+2>0”的充分不必要条件,是C正确;
对于D,命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,满足逆否命题的关系.
故选B.
点评:本题考查命题的真假的判断与应用,考查全称命题与特称命题的否定关系,复合命题的真假充要条件的判断,四种命题的逆否关系,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
过双曲线
-
=1的右焦点的直线交双曲线的右支于A,B两点,设F是双曲线的左焦点,e是双曲线的离心率,若△ABF为等腰三角形,且∠A=90°,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||
B、5-2
| ||
C、6-2
| ||
D、7-2
|
关于空间两条直线a、b和平面α,下列命题正确的是( )
| A、若a∥b,b?α,则a∥α |
| B、若a∥α,b?α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a∥α,b∥α,则a∥b |
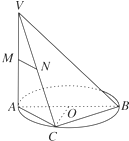 如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )
如图,AB是⊙O的直径,VA垂直⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
若椭圆
+
=1(a>b>0)的左、右焦点分别为F1、F2,椭圆上一点P,若|PF2|-|PF1|的最大值为2,且当P,F1,F2能构成三角形时,其周长为6,则椭圆方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|