题目内容
3.已知双曲线$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{m}$=1的一个焦点与抛物线x2=12y的焦点相同,则此双曲线的渐近线方程为( )| A. | y=±$\frac{\sqrt{5}}{5}$x | B. | y=±$\frac{2\sqrt{5}}{5}$x | C. | y=$±\frac{\sqrt{5}}{2}$x | D. | y=$±\sqrt{5}$x |
分析 求得抛物线的焦点,由题意可得3=$\sqrt{5+m}$,解方程可得m,可得双曲线的方程,再将其中的“1”换为“0”,进而得到所求渐近线方程.
解答 解:抛物线x2=12y的焦点为(0,3),
由双曲线$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{m}$=1的一个焦点与抛物线x2=12y的焦点相同,
可得3=$\sqrt{5+m}$,
解得m=4,
即有双曲线的方程为$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1,
可得渐近线方程为y=±$\frac{\sqrt{5}}{2}$x.
故选:C.
点评 本题考查双曲线的渐近线方程的求法,注意运用抛物线的焦点和双曲线的方程,考查运算能力,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
11.若双曲线$\frac{{x}^{2}}{3}$-$\frac{16{y}^{2}}{{p}^{2}}$=1的一个焦点在抛物线y2=2px的准线上,则该双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | 2 |
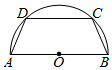 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.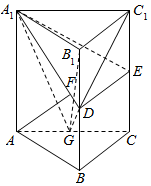 如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.