题目内容

8．若双曲线的方程为4x2-9y2=36，则其实轴长为6．

分析 将双曲线的方程化为标准方程，求得a，即可得到实轴长2a．

解答 解：双曲线的方程为4x2-9y2=36，即为：
$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1，
可得a=3，
则双曲线的实轴长为2a=6．
故答案为：6．

点评 本题考查双曲线的实轴长，注意将双曲线方程化为标准方程，考查运算能力，属于基础题．

练习册系列答案
相关题目
16．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{b}$=（-4，0），$\overrightarrow{c}$=（-1，-2），则-2$\overrightarrow{a}$+$\overrightarrow{b}$-3$\overrightarrow{c}$=（1，4）．
19．若双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$上一点P到点F1（-5，0）的距离是7，则点P到点F2（5，0）的距离是13．
16．双曲线$\frac{x^2}{m}-\frac{y^2}{4}=1$的焦点与椭圆$\frac{x^2}{20}+\frac{y^2}{4}=1$的焦点重合，则m的值等于（　　）
A．12B．20C．$2\sqrt{3}$D．$2\sqrt{5}$
3．已知双曲线$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{m}$=1的一个焦点与抛物线x2=12y的焦点相同，则此双曲线的渐近线方程为（　　）
A．y=±$\frac{\sqrt{5}}{5}$xB．y=±$\frac{2\sqrt{5}}{5}$xC．y=$±\frac{\sqrt{5}}{2}$xD．y=$±\sqrt{5}$x
13．双曲线2x2-y2=1的渐近线方程是y=±$\sqrt{2}$x，离心率是$\sqrt{3}$．
20．若直线l过点P（-3，-$\frac{3}{2}$）且被圆x2+y2=25截得的弦长是8，则直线l的方程为（　　）
A．3x+4y+15=0B．x=-3或3x+4y+15=0
C．x=-3或y=-$\frac{3}{2}$D．x=-3
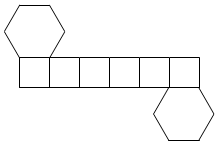17．已知函数f（x）=loga（2x-1）（a＞0，a≠1）在区间（0，1）内恒有f（x）＜0，则函数$y={log}_{a}（{x}^{2}-x+1）$的单调递减区间是$（-∞，\frac{1}{2}$）．
18．已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成，如图所示，若该凸多面体所有棱长均为1，则其体积V=$\frac{3\sqrt{3}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网