题目内容
18.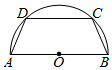 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A、B为焦点,且过C、D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为2$\sqrt{3}$-2.
分析 设∠BAC=θ,作CE⊥AB于点E,则可表示出BC,EB,CD,进而可求得梯形的周长的表达式,根据二次函数的性质求得周长的最大值时θ的值,则AC和BC可求,进而根据双曲线的定义求得双曲线的实轴长.
解答  解:设∠BAC=θ,作CE⊥AB于点E,
解:设∠BAC=θ,作CE⊥AB于点E,
则BC=2Rsinθ,EB=BCcos(90°-θ)=2Rsin2θ,
有CD=2R-4Rsin2θ,
梯形ABCD的周长l=AB+2BC+CD=2R+4Rsinθ+2R-4Rsin2θ
=8+8sinθ-8sin2θ=-8(sinθ-$\frac{1}{2}$)2+10,
当sinθ=$\frac{1}{2}$,即θ=30°时,l有最大值10,
即有BC=2,AC=2$\sqrt{3}$,a=$\frac{1}{2}$(AC-BC)=$\sqrt{3}$,
可得双曲线的实轴长为2a=2$\sqrt{3}$-2.
故答案为:2$\sqrt{3}$-2.
点评 本题主要考查了双曲线的应用,双曲线的定义.考查了学生分析问题和解决问题的能力,以及运算能力,属于中档题.

练习册系列答案
相关题目
13.经过点(3,-$\sqrt{2}$)的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,其一条渐近线方程为y=$\frac{\sqrt{3}}{3}$x,该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
3.已知双曲线$\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{m}$=1的一个焦点与抛物线x2=12y的焦点相同,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{\sqrt{5}}{5}$x | B. | y=±$\frac{2\sqrt{5}}{5}$x | C. | y=$±\frac{\sqrt{5}}{2}$x | D. | y=$±\sqrt{5}$x |
10.双曲线$\frac{y^2}{12}-\frac{x^2}{4}=1$的焦点到渐近线的距离为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
7.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3$\frac{1}{3}$寸,容纳米2000斛(1丈=10尺,l尺=10寸,斛为容积单位,l斛≈1.62立方尺,π≈3),则圆柱底圆周长约为( )
| A. | l丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48丈6尺 |