题目内容
17.当实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$时,ax+y+a+1≥0恒成立,则实数a的取值范围是$[-\frac{1}{2},+∞)$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义结合数形结合进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
直线ax+y+a-1=a(x+1)+(y+1)=0,过定点D(-1,-1).
ax+y+a+1≥0恒成立等价为可行域都在直线ax+y+a+1=0的上方;则由图象知只要B(1,0)满足ax+y+a+1≥0即可,
即2a+1≥0,得a≥$-\frac{1}{2}$,
故答案为:$[-\frac{1}{2},+∞)$;
点评 本题主要考查线性规划的应用,根据可行域与直线的关系结合数形结合是解决本题的关键.

练习册系列答案
相关题目
2.已知集合A={x|x2+x-6>0},集合B={x|-1<x<3},若a∈(A∪B),则a可以是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
9.已知A(1,-2),B(4,2),则与$\overrightarrow{AB}$反方向的单位向量为( )
| A. | (-$\frac{3}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{5}$,-$\frac{4}{5}$) | C. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | D. | ($\frac{3}{5}$,$\frac{4}{5}$) |
6.设复数z满足(1+i)z=-2i,i为虚数单位,则z=( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
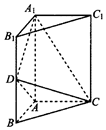 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.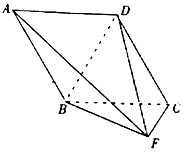 如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.
如图,平面ABCD⊥平面BCF,四边形ABCD是菱形,∠BCF=90°.