题目内容
8.函数f(x)=loga|x+1|在(-1,0)上是增函数,则f(x)在(-∞,-1)上是( )| A. | 函数值由负到正且为增函数 | B. | 函数值恒为正且为减函数 | ||
| C. | 函数值由正到负且为减函数 | D. | 没有单调性 |
分析 由已知分析出外函数的单调性,进而可得f(x)在(-∞,-1)上单调性和符号.
解答 解:内函数t=|x+1|在(-1,0)上是增函数,
若函数f(x)=loga|x+1|在(-1,0)上是增函数,
则外函数y=logat为增函数,
内函数t=|x+1|在(-∞,-1)上是减函数,
故f(x)在(-∞,-1)上是减函数,
又由f(-2)=0,
故f(x)在(-∞,-1)上是函数值由正到负且为减函数,
故选:C
点评 本题考查的知识点是复合函数的单调性,熟练掌握复合函数单调性“同增异减”的原则,是解答的关键.

练习册系列答案
相关题目
20.已知x>-1,则$x+\frac{4}{x+1}$的最小值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 已知函数f(x)=$\left\{\begin{array}{l}ax+b,x<0\\{2^x},x≥0\end{array}\right.$,且f(-2)=3,f(-1)=f(1).
已知函数f(x)=$\left\{\begin{array}{l}ax+b,x<0\\{2^x},x≥0\end{array}\right.$,且f(-2)=3,f(-1)=f(1).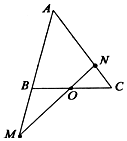 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).