��Ŀ����
2���躯��f��x��=lnx-$\frac{1}{2}a{x^2}$-bx����1����a=-2��b=3ʱ������f��x���ļ�ֵ��
��2����F��x��=f��x��+$\frac{1}{2}a{x^2}+bx+\frac{a}{x}��{0��x��3}��$����ͼ��������һ��P��x0��y0�������ߵ�б��k��$\frac{1}{2}$���������ʵ��a��ȡֵ��Χ��
��3����a=0��b=-1ʱ������f��x��=mx������[1��e2]��ǡ������ʵ���⣬��ʵ��m��ȡֵ��Χ��
���� ��1����a��b��ֵ����f��x�����������f��x���ĵ���������ڵ������ķ��̣���������ļ�ֵ���ɣ�
��2�����F��x���ĵ���������ת��Ϊa��${��-\frac{1}{2}x_0^2+{x_0}��_{min}}$���Ӷ����a�ķ�Χ���ɣ�
��3�����f��x���Ľ���ʽ������ת��Ϊm=1+$\frac{lnx}{x}$������[1��e2]��ǡ������ʵ���⣮
��� �⣺��1�������⣬f��x���Ķ�����Ϊ��0��+�ޣ���
��a=-2��b=3ʱ��f��x��=lnx+x2-3x����x��0����
f�䣨x��=$\frac{��2x-1����x-1��}{x}=0����x=\frac{1}{2}$��x=1
�б�f��x���ļ���ֵΪ$f��\frac{1}{2}��=-ln2-\frac{5}{4}$��
f��x���ļ�СֵΪf��1��=-2��
��2��F��x��=lnx+$\frac{a}{x}$��x�ʣ�0��3]��
����k=F'��x0��=$\frac{{{x_0}-a}}{{{x_0}^2}}��\frac{1}{2}$���ڣ�0��3]���н⣬
��a��${��-\frac{1}{2}x_0^2+{x_0}��_{min}}$
���� ��x=1ʱ��-$\frac{1}{2}x_0^2+{x_0}$ȡ����Сֵ$\frac{1}{2}$����a��$\frac{1}{2}$��
��3����a=0��b=-1ʱ��f��x��=lnx+x=mx����x��[1��e2]����
��m=1+$\frac{lnx}{x}��[{1��{e^2}}]������ʵ����$��
$m��[\frac{2}{e^2}+1��\frac{1}{e}+1��$ʱ����������ʵ���⣮
���� ���⿼���˺����ĵ����ԡ���ֵ���⣬���鵼����Ӧ���Լ�������������⣬��һ���е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | {x|x��0} | B�� | {x|x��1} | C�� | {x|x��2} | D�� | {x|x��1} |
 ��֪����f��x��=$\left\{\begin{array}{l}ax+b��x��0\\{2^x}��x��0\end{array}\right.$����f��-2��=3��f��-1��=f��1����
��֪����f��x��=$\left\{\begin{array}{l}ax+b��x��0\\{2^x}��x��0\end{array}\right.$����f��-2��=3��f��-1��=f��1����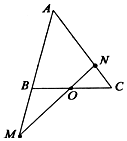 ��ͼ���ڡ�ABC�У���O��BC���е㣬����O��ֱ�߷ֱ�ֱ��AB��AC�ڲ�ͬ������M��N����$\overrightarrow{AM}=m\overrightarrow{AB}$��$\overrightarrow{AN}=n\overrightarrow{AC}��{mn��0}��$����m+n��ȡֵ��ΧΪ[2��+�ޣ���
��ͼ���ڡ�ABC�У���O��BC���е㣬����O��ֱ�߷ֱ�ֱ��AB��AC�ڲ�ͬ������M��N����$\overrightarrow{AM}=m\overrightarrow{AB}$��$\overrightarrow{AN}=n\overrightarrow{AC}��{mn��0}��$����m+n��ȡֵ��ΧΪ[2��+�ޣ��� ��ͼ����ƽ��������ABCD-A1B1C1D1�У�M��N�ֱ�����Խ���AC��A1C����CM=2MA��A1N=2ND��������$\overrightarrow{AB}=\overrightarrow a��\overrightarrow{AD}=\overrightarrow b��\overrightarrow{A{A_1}}=\overrightarrow c$����$\overrightarrow a��\overrightarrow b��\overrightarrow c$��ʾ$\overrightarrow{MN}$��
��ͼ����ƽ��������ABCD-A1B1C1D1�У�M��N�ֱ�����Խ���AC��A1C����CM=2MA��A1N=2ND��������$\overrightarrow{AB}=\overrightarrow a��\overrightarrow{AD}=\overrightarrow b��\overrightarrow{A{A_1}}=\overrightarrow c$����$\overrightarrow a��\overrightarrow b��\overrightarrow c$��ʾ$\overrightarrow{MN}$��