题目内容
6. 在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1
在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1与D1E所成角的余弦值为$\frac{\sqrt{15}}{30}$,AC1与平面EFG所成角的正弦值为$\frac{1}{3}$.
分析 建立如图所示的坐标系,设正方体的棱长为2,利用向量方法求出所求角.
解答 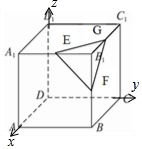 解:建立如图所示的坐标系,设正方体的棱长为2,可得A(2,0,0),C1(0,2,2),D1(0,0,2),E(2,1,2),F(2,2,1),G(1,2,2),则
解:建立如图所示的坐标系,设正方体的棱长为2,可得A(2,0,0),C1(0,2,2),D1(0,0,2),E(2,1,2),F(2,2,1),G(1,2,2),则
$\overrightarrow{A{C}_{1}}$=(-2,2,2),$\overrightarrow{{D}_{1}E}$=(2,1,0),
∴AC1与D1E所成角的余弦值为|$\frac{-4+2}{\sqrt{4+4+4}•\sqrt{4+1}}$|=$\frac{\sqrt{15}}{30}$;
平面EFG的一个法向量为(2,2,2),AC1与平面EFG所成角的正弦值为$\frac{-4+4+4}{2\sqrt{3}•2\sqrt{3}}$=$\frac{1}{3}$,
故答案为$\frac{\sqrt{15}}{30}$;$\frac{1}{3}$.
点评 本题考查线线角,考查线面角,考查向量方法的运用,属于中档题.

练习册系列答案
相关题目
14.不等式22x-1<2的解集是( )
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|x<2} | D. | {x|x<1} |
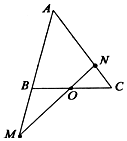 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).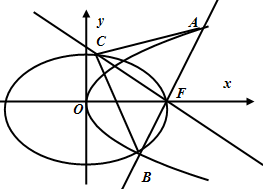 如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.
如图,设椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是$\frac{\sqrt{3}}{2}$.