题目内容
7.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与两条平行直线l1:y=x+b与l2:y=x-b分别相交于四点A,B,D,C,且四边形ABCD的面积为$\frac{{8{b^2}}}{3}$,则椭圆E的离心率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 联立直线与椭圆方程,求得A坐标,即求得边AB,利用点到直线的距离公式求得边AB上的高,即可表示面积,列式求解.
解答 解:如图所示,联立$\left\{\begin{array}{l}{y=x+b}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$⇒(a2+b2)x2+2ba2x=0,
可得点A的横坐标为$\frac{-2b{a}^{2}}{{a}^{2}+{b}^{2}}$.
∴AB=$\sqrt{2}$×$\frac{2b{a}^{2}}{{a}^{2}+{b}^{2}}$.
又因为原点到AB的距离d=$\frac{b}{\sqrt{2}}$
四边形ABCD的面积为AB×2d=$\sqrt{2}$×$\frac{2b{a}^{2}}{{a}^{2}+{b}^{2}}$×$\sqrt{2}b$=$\frac{8{b}^{2}}{3}$
整理得:a2=2b2,椭圆E的离心率为e=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$
故选:A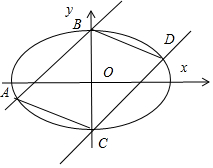
点评 本题考查了椭圆的离心率,涉及到了点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
18.若a=sin3,b=sin1.5,c=cos8.5,执行如图所示的程序框图,输出的是( )
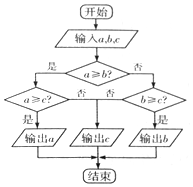

| A. | c | B. | b | C. | a | D. | $\frac{a+b+c}{3}$ |
15.已知函数$f(x)=sin(\frac{π}{3}-ωx)(ω>0)$向左平移半个周期得g(x)的图象,若g(x)在[0,π]上的值域为$[-\frac{{\sqrt{3}}}{2},1]$,则ω的取值范围是( )
| A. | $[\frac{1}{6},1]$ | B. | $[\frac{2}{3},\frac{3}{2}]$ | C. | $[\frac{1}{3},\frac{7}{6}]$ | D. | $[\frac{5}{6},\frac{5}{3}]$ |
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,若$\overrightarrow{b}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=2,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
19.从集合{2,3,4,5}中随机抽取一个数a,从集合{4,6,8}中随机抽取一个数b,则向量$\overrightarrow{m}$=(a,b)与向量$\overrightarrow{n}$=(-2,1)垂直的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
16.已知Sn为等差数列{an}的前n项和.若S9=18,则a3+a5+a7=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |