题目内容
15.已知函数$f(x)=sin(\frac{π}{3}-ωx)(ω>0)$向左平移半个周期得g(x)的图象,若g(x)在[0,π]上的值域为$[-\frac{{\sqrt{3}}}{2},1]$,则ω的取值范围是( )| A. | $[\frac{1}{6},1]$ | B. | $[\frac{2}{3},\frac{3}{2}]$ | C. | $[\frac{1}{3},\frac{7}{6}]$ | D. | $[\frac{5}{6},\frac{5}{3}]$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据ωx-$\frac{π}{3}$∈[-$\frac{π}{3}$,ωπ-$\frac{π}{3}$],f(x)在[0,π]上的值域为$[{-\frac{{\sqrt{3}}}{2},1}]$,可得$\frac{π}{2}$≤ωπ-$\frac{π}{3}$≤$\frac{4π}{3}$,由此求得ω的取值范围.
解答 解:函数$f(x)=sin(\frac{π}{3}-ωx)(ω>0)$=-sin(ωx-$\frac{π}{3}$)向左平移半个周期得
g(x)=-sin(ωx+ω•$\frac{1}{2}•\frac{2π}{ω}$-$\frac{π}{3}$)=sin(ωx-$\frac{π}{3}$)的图象,
由x∈[0,π],可得ωx-$\frac{π}{3}$∈[-$\frac{π}{3}$,ωπ-$\frac{π}{3}$],由于f(x)在[0,π]上的值域为$[{-\frac{{\sqrt{3}}}{2},1}]$.
即函数的最小值为$-\frac{{\sqrt{3}}}{2}$,最大值为1,则$\frac{π}{2}$≤ωπ-$\frac{π}{3}$≤$\frac{4π}{3}$,得$\frac{5}{6}≤ω≤\frac{5}{3}$.
综上,ω的取值范围是$[{\frac{5}{6},\frac{5}{3}}]$,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
3.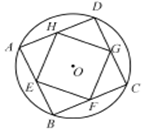 如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )
如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )
 如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )
如图,ABCD是以O为圆心、半径为2的圆的内接正方形,EFGH是正方形ABCD的内接正方形,且E、F、G、H分别为AB、BC、CD、DA的中点.将一枚针随机掷到圆O内,用M表示事件“针落在正方形ABCD内”,N表示事件“针落在正方形EFGH内”,则P(N|M)=( )| A. | $\frac{1}{π}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
10.已知集合P={x|x2-2x-8>0},Q={x|x≥a},P∪Q=R,则a的取值范围是( )
| A. | (-2,+∞) | B. | (4,+∞) | C. | (-∞,-2] | D. | (-∞,4] |
20.设i为虚数单位,若复数$\frac{z}{-i}$在复平面内对应的点为(1,2),则z=( )
| A. | -2+i | B. | 2-i | C. | -1+2i | D. | 1-2i |
7.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与两条平行直线l1:y=x+b与l2:y=x-b分别相交于四点A,B,D,C,且四边形ABCD的面积为$\frac{{8{b^2}}}{3}$,则椭圆E的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |