题目内容
17．在空间直角坐标系O-xyz中，四面体A-BCD在xOy，yOz，zOx坐标平面上的一组正投影图形如图所示（坐标轴用细虚线表示）．该四面体的体积是$\frac{8}{3}$．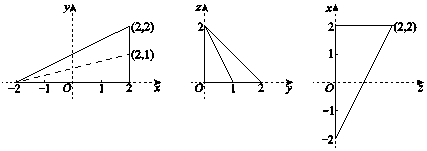
分析 根据三视图可得几何体的底面积和高，代入体积公式计算即可．
解答 解：由三视图可知几何体为三棱锥，
该三棱锥的底面积S底=$\frac{1}{2}×4×2$=4，高h=2，
∴V=$\frac{1}{3}×4×2$=$\frac{8}{3}$．
故答案为$\frac{8}{3}$．
点评 本题考查了棱锥的三视图，棱锥的体积计算，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
7．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）与两条平行直线l1：y=x+b与l2：y=x-b分别相交于四点A，B，D，C，且四边形ABCD的面积为$\frac{{8{b^2}}}{3}$，则椭圆E的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD为菱形，PC⊥平面ABCD，点E在棱PA上．
2．
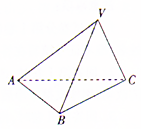如图所示，三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形，侧面VAC与底面ABC垂直，若以垂直于平面VAC的方向作为正视图的方向，垂直于平面ABC的方向为俯视图的方向，已知其正视图的面积为2$\sqrt{3}$，则其侧视图的面积是（ ）
如图所示，三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形，侧面VAC与底面ABC垂直，若以垂直于平面VAC的方向作为正视图的方向，垂直于平面ABC的方向为俯视图的方向，已知其正视图的面积为2$\sqrt{3}$，则其侧视图的面积是（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 3 |
9．已知集合A={x∈Z|x2-4x-5＜0}，B={x|4x＞2m}，若A∩B有三个元素，则实数m的取值范围是（ ）
| A． | [3，6） | B． | [1，2） | C． | [2，4） | D． | （2，4] |
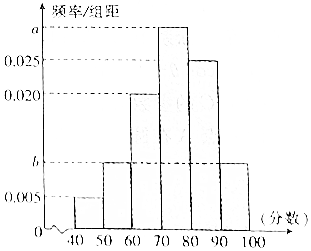某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图，其中前三段的频率成等比数列．