题目内容
12．已知等腰直角△ABC的斜边BC=2，沿斜边的高线AD将△ABC折起，使二面角B-AD-C为$\frac{π}{3}$，则四面体ABCD的外接球的表面积为$\frac{7π}{3}$．分析 由题意，△BCD是等边三角形，边长为1，外接圆的半径为$\frac{\sqrt{3}}{3}$，AD=1，可得四面体ABCD的外接球的半径=$\sqrt{\frac{1}{4}+\frac{1}{3}}$=$\sqrt{\frac{7}{12}}$，即可求出四面体ABCD的外接球的表面积．
解答 解：由题意，△BCD是等边三角形，边长为1，外接圆的半径为$\frac{\sqrt{3}}{3}$，
∵AD=1，∴四面体ABCD的外接球的半径=$\sqrt{\frac{1}{4}+\frac{1}{3}}$=$\sqrt{\frac{7}{12}}$，
∴四面体ABCD的外接球的表面积为$4π•\frac{7}{12}$=$\frac{7π}{3}$，
故答案为：$\frac{7π}{3}$．
点评 本题考查四面体ABCD的外接球的表面积，考查学生的计算能力，确定四面体ABCD的外接球的半径是关键．
练习册系列答案
相关题目
3．
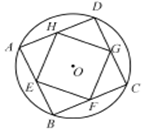如图，ABCD是以O为圆心、半径为2的圆的内接正方形，EFGH是正方形ABCD的内接正方形，且E、F、G、H分别为AB、BC、CD、DA的中点．将一枚针随机掷到圆O内，用M表示事件“针落在正方形ABCD内”，N表示事件“针落在正方形EFGH内”，则P（N|M）=（ ）
如图，ABCD是以O为圆心、半径为2的圆的内接正方形，EFGH是正方形ABCD的内接正方形，且E、F、G、H分别为AB、BC、CD、DA的中点．将一枚针随机掷到圆O内，用M表示事件“针落在正方形ABCD内”，N表示事件“针落在正方形EFGH内”，则P（N|M）=（ ）| A． | $\frac{1}{π}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
20．设i为虚数单位，若复数$\frac{z}{-i}$在复平面内对应的点为（1，2），则z=（ ）
| A． | -2+i | B． | 2-i | C． | -1+2i | D． | 1-2i |
7．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）与两条平行直线l1：y=x+b与l2：y=x-b分别相交于四点A，B，D，C，且四边形ABCD的面积为$\frac{{8{b^2}}}{3}$，则椭圆E的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
17．设x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-1≥0\\ x≤3\end{array}\right.$，则z=2x-3y的最大值是（ ）
| A． | -3 | B． | -6 | C． | 15 | D． | 12 |
如图，四边形ABCD为直角梯形，∠ABC=90°，CB∥DA，AB=20$\sqrt{2}$，DA=10，CB=20，若AB边上有一点P，使得∠CPD最大，则AP=10$\sqrt{2}$．
2．
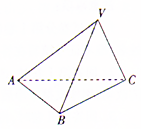如图所示，三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形，侧面VAC与底面ABC垂直，若以垂直于平面VAC的方向作为正视图的方向，垂直于平面ABC的方向为俯视图的方向，已知其正视图的面积为2$\sqrt{3}$，则其侧视图的面积是（ ）
如图所示，三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形，侧面VAC与底面ABC垂直，若以垂直于平面VAC的方向作为正视图的方向，垂直于平面ABC的方向为俯视图的方向，已知其正视图的面积为2$\sqrt{3}$，则其侧视图的面积是（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 3 |