题目内容
从1到9的九个数字中取三个偶数四个奇数,试问:
(Ⅰ)能组成多少个没有重复数字的七位数?
(Ⅱ)在(Ⅰ)中的七位数中三个偶数排在一起的有几个?
(Ⅲ)在(Ⅰ)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(Ⅰ)能组成多少个没有重复数字的七位数?
(Ⅱ)在(Ⅰ)中的七位数中三个偶数排在一起的有几个?
(Ⅲ)在(Ⅰ)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
考点:计数原理的应用
专题:排列组合
分析:(Ⅰ)本题是一个分步计数问题,第一步在4个偶数中取3个,有C43种结果,第二步在5个奇数中取4个,有C54种结果,第三步得到的7个数字进行排列有A77种结果,根据分步计数原理得到结果.
(Ⅱ)上述七位数中三个偶数排在一起可以把三个偶数看成一个元素进行排列,三个元素之间还有一个排列,得到结果.
(Ⅲ)由(1)第一、二步,将3个偶数排在一起,有A33种情况,4个奇数也排在一起有A44种情况,将奇数与偶数进行全排列计算可得答案.
(Ⅱ)上述七位数中三个偶数排在一起可以把三个偶数看成一个元素进行排列,三个元素之间还有一个排列,得到结果.
(Ⅲ)由(1)第一、二步,将3个偶数排在一起,有A33种情况,4个奇数也排在一起有A44种情况,将奇数与偶数进行全排列计算可得答案.
解答:
解:(Ⅰ)由题意知本题是一个分步计数问题,
第一步在4个偶数中取3个,有C43种结果,
第二步在5个奇数中取4个,有C54种结果,
第三步得到的7个数字进行排列有A77种结果,
∴符合题意的七位数有C43C54A77=100800.
(Ⅱ)上述七位数中,三个偶数排在一起可以把三个偶数看成一个元素进行排列,
三个元素之间还有一个排列,有C43C54A55A33=14400.
(Ⅲ)上述七位数中,3个偶数排在一起有A33种情况,4个奇数也排在一起有A44种情况,
共有C43C54A33A44A22=5760个.
第一步在4个偶数中取3个,有C43种结果,
第二步在5个奇数中取4个,有C54种结果,
第三步得到的7个数字进行排列有A77种结果,
∴符合题意的七位数有C43C54A77=100800.
(Ⅱ)上述七位数中,三个偶数排在一起可以把三个偶数看成一个元素进行排列,
三个元素之间还有一个排列,有C43C54A55A33=14400.
(Ⅲ)上述七位数中,3个偶数排在一起有A33种情况,4个奇数也排在一起有A44种情况,
共有C43C54A33A44A22=5760个.
点评:本题考查排列组合及简单计数问题,本题解题的关键是对于要求相邻的元素要采用捆绑法,对于不相邻的元素要采用插空法,本题是一个比较典型的排列组合问题

练习册系列答案
相关题目
函数f(x)=ln(x+1)-
+1的零点所在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
观察下面的演绎推理过程,判断正确的是( )
大前提:若直线a⊥直线 l,且直线b⊥直线 l,则a∥b.
小前提:正方体 ABCD-A1B1C1D1中,A1B1⊥AA1.且AD⊥AA1
结论:A1B1∥AD.
大前提:若直线a⊥直线 l,且直线b⊥直线 l,则a∥b.
小前提:正方体 ABCD-A1B1C1D1中,A1B1⊥AA1.且AD⊥AA1
结论:A1B1∥AD.
| A、推理正确 |
| B、大前提出错导致推理错误 |
| C、小前提出错导致推理错误 |
| D、仅结论错误 |
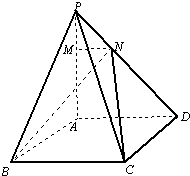 已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2
已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2 在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为