题目内容
4.函数f(x)=${log_{\frac{1}{3}}}(1-{x^2})$的单调递增区间是[0,1).分析 令t=1-x2>0,求得函数的定义域,f(x)=g(t)=${log}_{\frac{1}{3}}t$,本题即求函数t在定义域内的减区间.再利用二次函数的性质可得结论.
解答 解:令t=1-x2>0,求得函数的定义域为{x|-1<x<1},f(x)=g(t)=${log}_{\frac{1}{3}}t$,
故本题即求函数t在定义域内的减区间.
再利用二次函数的性质可得t在定义域内的减区间为[0,1),
故答案为:[0,1).
点评 本题主要考查复合函数的单调性,对数函数、二次函数的性质,属于基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
12.如果函数f(x)=x2+ax+2在区间[2,+∞)上是增函数,那么实数a的取值范围是( )
| A. | a≤-2 | B. | a≥-2 | C. | a≤-4 | D. | a≥-4 |
9.等比数列{an}中,${a_1}+{a_2}+{a_3}+…+{a_n}={2^n}-1$,则$\frac{1}{a_1^2}+\frac{1}{a_2^2}+\frac{1}{a_3^2}+…+\frac{1}{a_n^2}$=( )
| A. | (2n-1)2 | B. | $\frac{1}{3}({2^n}-1)$ | C. | $\frac{1}{3}(4-\frac{1}{{{4^{n-1}}}})$ | D. | $\frac{1}{3}({4^n}-1)$ |
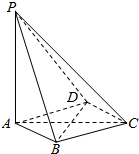 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.