题目内容
19.定义:区间[x1,x2](x1<x2)的长度为x2-x1,已知函数y=|log0.5(x+1)|定义域为[a,b],值域为[0,2],则区间[a,b]的长度的最大值为$\frac{15}{4}$.分析 由0≤|log0.5(x+1)|≤2解得-$\frac{3}{4}$≤x≤3,从而求最值.
解答 解:∵0≤|log0.5(x+1)|≤2,
∴-2≤log0.5(x+1)≤2,
∴$\frac{1}{4}$≤x+1≤4,
∴-$\frac{3}{4}$≤x≤3,
∴区间[a,b]的长度的最大值为
3+$\frac{3}{4}$=$\frac{15}{4}$;
故答案为:$\frac{15}{4}$.
点评 本题考查了绝对值不等式的解法及整体思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在等差数列{an}中,a2=4,a4=2,则a8=( )
| A. | -1 | B. | -2 | C. | 4 | D. | 8 |
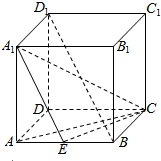 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.