题目内容
已知函数f（x）=-2| 3 |
| 3 |
（Ⅰ）求函数f（x）的最小正周期和单调增区间；
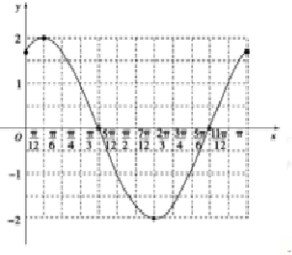
（Ⅱ）在给出的直角坐标系中，画出函数y=f（x）在区间[0，π]上的图象．
考点：五点法作函数y=Asin（ωx+φ）的图象
专题：作图题
分析：（Ⅰ）从函数f（x）变形为2sin（2x+
）进而直接求出最小正周期和单调增区间；
（Ⅱ）先列表再在给出的直角坐标系中描点连线进而画出函数y=f（x）在区间[0，π]上的图象．
| π |
| 3 |
（Ⅱ）先列表再在给出的直角坐标系中描点连线进而画出函数y=f（x）在区间[0，π]上的图象．
解答：
解：（1）f（x）=
（1-2sin2x）+sin 2x
=sin 2x+
cos 2x=2sin（2x+
），
所以f（x）的最小正周期T=
=π．
由2kπ-
＜2x+
＜2kπ+
得kπ-
＜2x+
＜kπ+
所以f（x）的单调增区间为[kπ-
，kπ+
]（k∈Z）
（2）列表：
描点连线得图象，如图所示．
| 3 |
=sin 2x+
| 3 |
| π |
| 3 |
所以f（x）的最小正周期T=
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 3 |
| π |
| 12 |
所以f（x）的单调增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
（2）列表：
| x | 0 |
|
|
|
| π | ||||||||||
2x+
|
|
| π |
| 2π |
| ||||||||||
| f（x） |
| 2 | 0 | -2 | 0 |
|
点评：本题考查三角函数的变换技巧、最小正周期、单调增区间及五点作图法，是中档题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
