题目内容
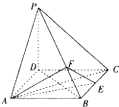如图，ABCD是正方形，PD⊥平面ABCD，点E是BC中点，点F在PB上，且PE=2FB．（1）求证：AC⊥平面AEF；
（2）求证：PD∥平面AEF．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）由线面垂直的判定定理进行判定，（2）设AE交BD于G，得
=
=
，连接FG，有FG∥PD，FG?AEB，PD?AEF，从而得出线面平行．
| BF |
| FP |
| 1 |
| 2 |
| BG |
| DG |
解答：
证明：（1）∵PD⊥平面ABCD，
∴PD⊥AC，
∵ABCD是正方形，
∴AC⊥BD，
∴AC⊥平面PBD；
（2）设AE交BD于G，
∵点E是BC中点，ABCD是正方形，
∴
=
=
，
∵PF=2FB，∴
=
=
，
∴连接FG，有FG∥PD，
∵FG?AEB，PD?AEF，
∴PD∥平面AEF．
∴PD⊥AC，
∵ABCD是正方形，
∴AC⊥BD，
∴AC⊥平面PBD；
（2）设AE交BD于G，
∵点E是BC中点，ABCD是正方形，
∴
| BG |
| DG |
| BE |
| AD |
| 1 |
| 2 |
∵PF=2FB，∴
| BF |
| FP |
| 1 |
| 2 |
| BG |
| DG |
∴连接FG，有FG∥PD，
∵FG?AEB，PD?AEF，
∴PD∥平面AEF．
点评：本题考查了线面垂直，线面平行的判定，牢记并理解判定定理是证明的关键．
练习册系列答案
相关题目
命题“任何一个实数与其相反数的和都是零”的否定是（ ）
| A、任何一个实数与其相反数的和都不是零 |
| B、任何一个实数与其相反数的差都是零 |
| C、存在一个实数与其相反数的差都是零 |
| D、存在一个实数与其相反数的和不为零 |