题目内容
设f（tanx）=tan2x，则f（2）等于 ．
考点：二倍角的正切,函数解析式的求解及常用方法
专题：三角函数的求值
分析：由条件利用二倍角的正切公式可得f（t）=
，从而求得f（2）的值．
| 2t |
| 1-t2 |
解答：
解：令t=tanx，∵f（tanx）=tan2x=
，∴f（t）=
，
故f（2）=
=-
，
故答案为：-
．
| 2tanx |
| 1-tan2x |
| 2t |
| 1-t2 |
故f（2）=
| 4 |
| 1-4 |
| 4 |
| 3 |
故答案为：-
| 4 |
| 3 |
点评：本题主要考查二倍角的正切公式的应用，求函数的解析式，属于基础题．
练习册系列答案
相关题目
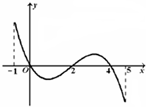已知函数y=f（x）的定义域为[-1，5]，部分对应值如下表，y=f（x）的导函数y=f′（x）的图象如图所示．下列关于y=f（x）的命题：