题目内容
3.二项式(1-x)6的展开式中x2的系数是( )| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
分析 先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中x2的系数.
解答 解:二项式(1-x)6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-x)r,
令r=2,可得展开式中x2的系数是${C}_{6}^{2}$=15,
故选:C.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
14.已知a,b,c∈R,则“a>0且b2-4ac<0”是“?x∈R,都有ax2+bx+c≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.某程序框图如图所示,则该程序运行后输出的值是( )


| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
15.已知M=a+$\frac{1}{a-1}$(a>1),N=3${\;}^{1-{x}^{2}}$(x∈R),则M,N的大小关系为( )
| A. | M≥N | B. | M>N | C. | M<N | D. | M≤N |
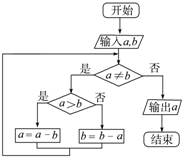 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,20,则输出的a=2.