题目内容
13.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=2x,若存在x0∈[1,2]使得等式af(x0)+g(2x0)=0成立,则实数a的取值范围是[$\frac{17}{6},\frac{257}{60}$].分析 根据函数奇偶性,解出奇函数f(x)和偶函数g(x)的表达式,将等式af(x)+g(2x)=0,令t=2x-2-x,则t>0,通过变形可得a=t+$\frac{2}{t}$,讨论出右边在x∈[1,2]的最大值,可以得出实数a的取值范围.
解答 解:解:∵f(x)为定义在R上的奇函数,g(x)为定义在R上的偶函数,
∴f(-x)=-f(x),g(-x)=g(x),
又∵由f(x)+g(x)=2-x,结合f(-x)+g(-x)=-f(x)+g(x)=2x,
∴f(x)=-$\frac{1}{2}$(2x-2-x),g(x)=$\frac{1}{2}$(2x+2-x).
等式af(x)+g(2x)=0,化简为-$\frac{a}{2}$(2x-2-x)+$\frac{1}{2}$(22x+2-2x)=0.
∵x∈[1,2],∴$\frac{3}{2}$≤2x-2-x≤$\frac{15}{4}$,
令t=2x-2-x,则t>0,因此将上面等式整理,得:a=t+$\frac{2}{t}$,
函数h(t)=t+$\frac{2}{t}$在[$\frac{3}{2}$$,\frac{15}{4}$]递增,$\frac{17}{6}$≤t+$\frac{2}{t}$≤$\frac{257}{60}$,
则实数a的取值范围是[$\frac{17}{6},\frac{257}{60}$],
故答案为:[$\frac{17}{6},\frac{257}{60}$].
点评 题以指数型函数为载体,考查了函数求表达式以及不等式恒成立等知识点,属于难题.合理地利用函数的基本性质,再结合换元法和基本不等式的技巧,是解决本题的关键.属于中档题

练习册系列答案
相关题目
1.已知i是虚数单位,复数z满足$\frac{z}{2+z}=i$,则复数z在复平面内对应的点的坐标是( )
| A. | $(-\frac{1}{2},\frac{1}{2})$ | B. | (-1,1) | C. | $(\frac{1}{2},-\frac{1}{2})$ | D. | (1,-1) |
8.如果实数x,y满足约束条件$\left\{\begin{array}{l}{3x+y-6≤0}\\{x-y-2≤0}\\{x≥1}\end{array}\right.$,则z=$\frac{y+1}{x+1}$的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
18.函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象与$g(x)=2co{s^2}({x-\frac{π}{6}})+1$的图象的对称轴相同,则f(x)的一个递增区间为( )
| A. | $[{-\frac{5π}{6},\frac{π}{6}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{5π}{12},\frac{π}{12}}]$ | D. | $[{\frac{π}{12},\frac{7π}{12}}]$ |
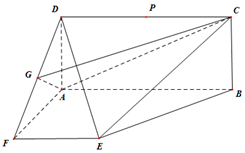 已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.
已知矩形ABCD与直角梯形ABEF,∠DAF=∠FAB=90°,点G为DF的中点,AF=EF=$\frac{1}{2}AB=\sqrt{3}$,P在线段CD上运动.