题目内容
6.若存在实数x使|x-a|+|x|≤4成立,则实数a的取值范围是[-4,4].分析 利用绝对值的几何意义,可得到|a|≤4,解之即可.
解答 解:在数轴上,|x-a|表示横坐标为x的点P到横坐标为a的点A距离,
|x|就表示点P到横坐标为0的点B的距离,
∵(|PA|+|PB|)min=|a|,
∴要使得不等式|x-a|+|x|≤4成立,只要最小值|a|≤4就可以了,
∴-4≤a≤4.
故实数a的取值范围是-4≤a≤4.
故答案为:[-4,4].
点评 本题考查绝对值不等式的解法,考查绝对值的几何意义,得到|a|≤4是关键,也是难点.

练习册系列答案
相关题目
14.已知实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+2y≤6\\ 3x+y≤12\end{array}\right.$,且x,y∈Z,则z=2x+y的最大值是( )
| A. | 7 | B. | 8 | C. | $\frac{42}{5}$ | D. | 9 |
1.执行如图所示的程序框图,则输出s的值为( )
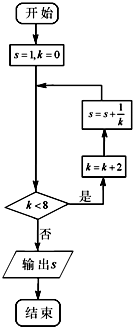

| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{23}{12}$ | D. | $\frac{49}{24}$ |
11.若a,b∈N,则$\frac{1}{a}$+$\frac{1}{b}$>1成立的充要条件是( )
| A. | a,b都不大于2 | B. | a,b中至少有一个等于1 | ||
| C. | a,b都大于2 | D. | a,b中至多有一个等于1 |
15.函数y=9-x2( )
| A. | 有最大值-9 | B. | 有最小值9 | C. | 有最大值9 | D. | 有最小值-9 |
7.从四面体ABCD的6条棱的中点及其四个顶点共10个点中任取4个点,则这四个点不共面的概率是( )
| A. | $\frac{5}{7}$ | B. | $\frac{7}{10}$ | C. | $\frac{24}{35}$ | D. | $\frac{47}{70}$ |