题目内容
17.观察下列等式:a2-b2=(a-b)(a+b)
a3-b3=(a-b)(a2+ab+b2)
a4-b4=(a-b)(a3+a2b+ab2+b3),…,
照此规律,an-bn=(a-b)(an-1+an-2b+…+abn-2+bn-1)(n≥2,n∈N)
分析 根据所给信息,可知各个等式的左边两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列,故可得答案.
解答 解:由题意,当n=1时,有(a-b)(a+b)=a2-b2;
当n=2时,有(a-b)(a2+ab+b2)=a3-b3;
当n=3时,有(a-b)(a3+a2b+ab2+b3)=a4-b4;
当n=4时,有(a-b)(a4+a3b+a2b2+ab3+b4)=a5-b5;
所以得到猜想:当n∈N*时,有(a-b)(an-1+an-2b+…+abn-2+bn-1)=an-bn;
故答案为(a-b)(an-1+an-2b+…+abn-2+bn-1).
点评 本题的考点是归纳推理,主要考查信息的处理,关键是根据所给信息,可知两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.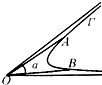 如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
 如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
5.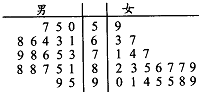 某大学为了在2016年全国大学生成语听写大赛取得优秀成绩,抽调男女各20名学生组成集训队进行成语听写集训,集训结束时,为了检验集训效果,对所有集训队员进行成语听写考核,试题为听写100个常用成语(每个1分,满分100分),考核成绩如图茎叶图所示:
某大学为了在2016年全国大学生成语听写大赛取得优秀成绩,抽调男女各20名学生组成集训队进行成语听写集训,集训结束时,为了检验集训效果,对所有集训队员进行成语听写考核,试题为听写100个常用成语(每个1分,满分100分),考核成绩如图茎叶图所示:
(I)若大于或等于80分为优秀队员,80分以下为非优秀队员,根据茎叶图填写下面2×2列联表,并判断能否有95%的把握认为队员的优秀与性别有关?
(Ⅱ)若从考核成绩95分以上(包括95分)的队员中任选两人代表这所大学参加全国大学生成语听写大赛,求至少有一名男队员参加的概率.
下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 某大学为了在2016年全国大学生成语听写大赛取得优秀成绩,抽调男女各20名学生组成集训队进行成语听写集训,集训结束时,为了检验集训效果,对所有集训队员进行成语听写考核,试题为听写100个常用成语(每个1分,满分100分),考核成绩如图茎叶图所示:
某大学为了在2016年全国大学生成语听写大赛取得优秀成绩,抽调男女各20名学生组成集训队进行成语听写集训,集训结束时,为了检验集训效果,对所有集训队员进行成语听写考核,试题为听写100个常用成语(每个1分,满分100分),考核成绩如图茎叶图所示:(I)若大于或等于80分为优秀队员,80分以下为非优秀队员,根据茎叶图填写下面2×2列联表,并判断能否有95%的把握认为队员的优秀与性别有关?
| 非优秀 | 优秀 | 总数 | |
| 男 | 20 | ||
| 女 | 20 | ||
| 总数 | 40 |
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12.已知抛物线y2=4x的准线与双曲线4x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线离心率为( )
| A. | $\frac{\sqrt{17}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\frac{\sqrt{57}}{3}$ | D. | $\frac{8}{3}$ |
2.设p:?x0∈R,mx02+1≤0,q:x∈R,x2+mx+1>0,若p∨q为真命题,则实数m的取值范围是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (-2,2) | D. | (-∞,2]∪[2,+∞) |
9.圆x2+(y-m)2=5与双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线相切,则正实数m=( )
| A. | 5 | B. | 1 | C. | 5$\sqrt{5}$ | D. | $\sqrt{5}$ |
7.已知$cos(\frac{π}{2}+φ)=\frac{3}{5}$,且$|φ|<\frac{π}{2}$,则tanφ为( )
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
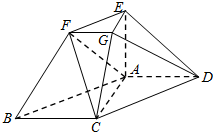 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.