题目内容
14．已知实数x，y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+2y≤6\\ 3x+y≤12\end{array}\right.$，且x，y∈Z，则z=2x+y的最大值是（ ）| A． | 7 | B． | 8 | C． | $\frac{42}{5}$ | D． | 9 |
分析 画出不等式标示的区域，找出区域内的所有整点，检验可得z=2x+y的最大值．
解答 
解：做出不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+2y≤6\\ 3x+y≤12\end{array}\right.$，且x，y∈Z表示的区域，
得到如图的四边形OABC及其内部的整点，
其中，A（0，3），B（$\frac{18}{5}$，$\frac{6}{5}$），C（4，0），0为坐标原点，
由于x，y∈Z，而区域内的所有整点为（0，0）、（0，1）、
（0，2）、（0，3）、（1，1）、（1，2）、（2，0）、（2，1）、（2，2）、（3，0）、（3，1），
故当直线l经过点（3，1）时，z=2x+y取得最大值为7，
故选：A．
点评 本题给出二元一次不等式组，求目标函数z=2x+y的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．
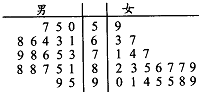某大学为了在2016年全国大学生成语听写大赛取得优秀成绩，抽调男女各20名学生组成集训队进行成语听写集训，集训结束时，为了检验集训效果，对所有集训队员进行成语听写考核，试题为听写100个常用成语（每个1分，满分100分），考核成绩如图茎叶图所示：
（I）若大于或等于80分为优秀队员，80分以下为非优秀队员，根据茎叶图填写下面2×2列联表，并判断能否有95%的把握认为队员的优秀与性别有关？
（Ⅱ）若从考核成绩95分以上（包括95分）的队员中任选两人代表这所大学参加全国大学生成语听写大赛，求至少有一名男队员参加的概率．
下面的临界值表供参考：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
某大学为了在2016年全国大学生成语听写大赛取得优秀成绩，抽调男女各20名学生组成集训队进行成语听写集训，集训结束时，为了检验集训效果，对所有集训队员进行成语听写考核，试题为听写100个常用成语（每个1分，满分100分），考核成绩如图茎叶图所示：（I）若大于或等于80分为优秀队员，80分以下为非优秀队员，根据茎叶图填写下面2×2列联表，并判断能否有95%的把握认为队员的优秀与性别有关？
| 非优秀 | 优秀 | 总数 | |
| 男 | 20 | ||
| 女 | 20 | ||
| 总数 | 40 |
下面的临界值表供参考：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
2．设p：?x0∈R，mx02+1≤0，q：x∈R，x2+mx+1＞0，若p∨q为真命题，则实数m的取值范围是（ ）
| A． | （-∞，2） | B． | （2，+∞） | C． | （-2，2） | D． | （-∞，2]∪[2，+∞） |
9．圆x2+（y-m）2=5与双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线相切，则正实数m=（ ）
| A． | 5 | B． | 1 | C． | 5$\sqrt{5}$ | D． | $\sqrt{5}$ |
3．某几何体三视图如图所示，则该几何体的最短的棱长度是（ ）
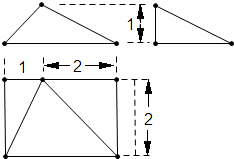
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |