题目内容
18．已知函数f（x）=log2x，g（x）=$\left\{\begin{array}{l}{f（x），x≥2}\\{f（4-x），x＜2}\end{array}\right.$若关于x的方程g（x）=k有两个不相等的实数根，则实数k的取值范围是（1，+∞）．分析 求出g（x）的解析式，由题意可得函数y=g（x）和y=k图象由两个交点，画出函数y=g（x）的图象和直线y=k，通过图象即可得到所求范围．
解答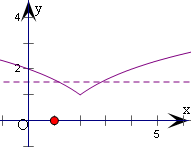 
解：函数f（x）=log2x，
g（x）=$\left\{\begin{array}{l}{f（x），x≥2}\\{f（4-x），x＜2}\end{array}\right.$即g（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x≥2}\\{lo{g}_{2}（4-x），x＜2}\end{array}\right.$，
关于x的方程g（x）=k有两个不相等的实数根，
即函数y=g（x）和y=k图象由两个交点，
画出函数y=g（x）的图象和直线y=k，
由图象可得，实数k的取值范围为（1，+∞）．
故答案为：（1，+∞）．
点评 本题考查函数方程的转化思想的运用，考查数形结合的思想方法，属于中档题．
练习册系列答案
相关题目
8．
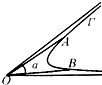如图，曲线Γ在顶点为O的角α的内部，A、B是曲线Γ上任意相异两点，且α≥∠AOB，我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”．已知O为坐标原点，曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}（x≤0）}\\{2{x}^{2}-3x+2（x＞0）}\end{array}\right.$，那么它相对于点O的“确界角”等于（ ）
如图，曲线Γ在顶点为O的角α的内部，A、B是曲线Γ上任意相异两点，且α≥∠AOB，我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”．已知O为坐标原点，曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}（x≤0）}\\{2{x}^{2}-3x+2（x＞0）}\end{array}\right.$，那么它相对于点O的“确界角”等于（ ）| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{7π}{12}$ |
9．圆x2+（y-m）2=5与双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线相切，则正实数m=（ ）
| A． | 5 | B． | 1 | C． | 5$\sqrt{5}$ | D． | $\sqrt{5}$ |
13．执行如图的程序框图，如果输入的n是3，那么输出的p是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{24}$ | D． | $\frac{1}{120}$ |
3．某几何体三视图如图所示，则该几何体的最短的棱长度是（ ）
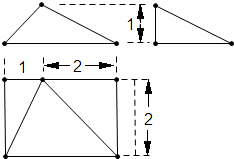
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
7．已知$cos（\frac{π}{2}+φ）=\frac{3}{5}$，且$|φ|＜\frac{π}{2}$，则tanφ为（ ）
| A． | $-\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | $-\frac{3}{4}$ | D． | $\frac{3}{4}$ |