题目内容
4.已知定义在R上的偶函数f(x)满足f(x+4)=f(x),且当0≤x≤2时,f(x)=min{-x2+2x,2-x},若方程f(x)-mx=0恰有两个根,则m的取值范围是( )| A. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) | B. | [-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) | C. | (-2,-$\frac{1}{3}$)∪($\frac{1}{3}$,2) | D. | [-2,-$\frac{1}{3}$]∪[$\frac{1}{3}$,2] |
分析 首先由题意求出f(x),然后令g(x)=mx,转化为图象交点的问题解决.
解答 解:由题意得f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,0≤x≤1}\\{2-x,1<x≤2}\end{array}\right.$,
又因为f(x)是偶函数且周期是4,可得整个函数的图象,
令g(x)=mx,本题转化为两个交点的问题,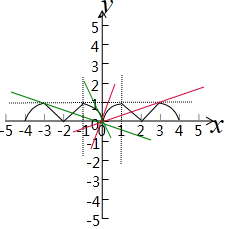 ,
,
结合图象,-2<m<-$\frac{1}{3}$或$\frac{1}{3}$<m<2,
故选:C.
点评 本题考查的是函数的性质的综合应用,利用数形结合快速得解.

练习册系列答案
相关题目
17.在函数 ①y=cos|2x|,②y=|cosx|,③$y=|sin(2x+\frac{π}{2})|$,④y=tan|x|中,最小正周期为π的所有偶 函数为( )
| A. | ①② | B. | ①②③ | C. | ②④ | D. | ①③ |
18.某班一个学习小组在一次数学实践活动中,测得一组数据共5个,如表
若x1+x2+x3+x4=10,计算得回归方程为$\stackrel{∧}{y}$=2.5x-2.3,则n的值为( )
| x | x1 | x2 | x3 | x4 | 5 |
| y | 2.5 | 4.6 | 5.4 | n | 7.5 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
13.变量x,y之间的一组相关数据如表所示:
若x,y之间的线性回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+12.28,则$\stackrel{∧}{b}$的值为( )
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.96 | B. | -0.94 | C. | -0.92 | D. | -0.98 |
14.某高校调查询问了56名男女大学生在课余时间是否参加运动,得到下表所示的数据.从表中数据分析,有多大把握认为大学生的性别与参加运动之间有关系.
| 参加运动 | 不参加运动 | 合计 | |
| 男大学生 | 20 | 8 | 28 |
| 女大学生 | 12 | 16 | 28 |
| 合计 | 32 | 24 | 56 |