题目内容
12.已知等比数列{an}的前n项和为Sn,${a_2}=-\frac{1}{2}$,且满足Sn,Sn+2,Sn+1成等差数列,则a3等于$\frac{1}{4}$.分析 由已知结合等差数列的定义可得,Sn+2-Sn=Sn+1-Sn+2,从而可得an+2与an+1的递推关系,结合等比数列的通项可求a3.
解答 解:∵Sn、Sn+2、Sn+1成等差数列,
∴Sn+2-Sn=Sn+1-Sn+2.
∴an+2+an+1=-an+2,
∴公比q=$\frac{{a}_{n+2}}{{a}_{n+1}}$=-$\frac{1}{2}$,
又a2=-$\frac{1}{2}$,
∴a3=a2q=(-$\frac{1}{2}$)2=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查了利用数列的递推关系构造等比数列求解数列的通项公式,考查等比数列的通项公式的运用,运算能力,属于基础题.

练习册系列答案
相关题目
3.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤0}\\{2x-y≤4}\end{array}\right.$,则目标函数z=2x+3y的最小值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
7.在平面直角坐标系xoy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$(θ为参数),则过点(3,0)且斜率为$\frac{4}{5}$的直线l被曲线C截得的线段中点的坐标为( )
| A. | (-$\frac{3}{2}$,-$\frac{18}{5}$) | B. | ($\frac{4}{3}$,-$\frac{4}{3}$) | C. | (-2,-4) | D. | ($\frac{3}{2}$,-$\frac{6}{5}$) |
4.已知定义在R上的偶函数f(x)满足f(x+4)=f(x),且当0≤x≤2时,f(x)=min{-x2+2x,2-x},若方程f(x)-mx=0恰有两个根,则m的取值范围是( )
| A. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) | B. | [-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) | C. | (-2,-$\frac{1}{3}$)∪($\frac{1}{3}$,2) | D. | [-2,-$\frac{1}{3}$]∪[$\frac{1}{3}$,2] |
1.在△ABC中,已知角A,B,C的对边分别为a,b,c.若a=2,A=30°,C=45°,则△ABC的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$+1 | C. | $\frac{1}{2}$($\sqrt{3}$+1) | D. | 2$\sqrt{2}$ |
2.已知a,b,c是互不相等的非零实数,若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+c=0至少有一个方程有两个相异实根,反证假设应为( )
| A. | 三个方程中至多有一个方程有两个相异实根 | |
| B. | 三个方程都有两个相异实根 | |
| C. | 三个方程都没有两个相异实根 | |
| D. | 三个方程都没有实根 |
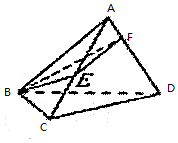 如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.
如图,在正四面体A-BCD中,所有棱长为1,E,F分别是AC,AD上的动点,求截面△BEF周长的最小值.