题目内容
6.已知tanα=2,则sin2($\frac{π}{2}$+α)-sin(3π+α)cos(2π-α)=$\frac{3}{5}$.分析 利用诱导公式,同角三角函数基本关系式化简所求,代入tanα=2计算即可得解.
解答 解:∵tanα=2,
∴sin2($\frac{π}{2}$+α)-sin(3π+α)cos(2π-α)
=cos2α+sinαcosα
=$\frac{co{s}^{2}α+sinαcosα}{co{s}^{2}α+si{n}^{2}α}$
=$\frac{1+tanα}{1+ta{n}^{2}α}$
=$\frac{1+2}{1+4}$
=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
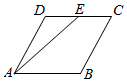
17.如图,在菱形ABCD中,AB=2,∠DAB=60°,E为CD的中点,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的值是( )

| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
14.如图所示,当输入a,b分别为2,3时,最后输出的m的值是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知集合A={x∈R|0<x<2},则∁RA=( )
| A. | {x|x≤0} | B. | {x|x≥2} | C. | {x|x<0或x>2} | D. | {x|x≤0或x≥2} |
11.观察这列数:1,2,3,3,2,1,2,3,4,4,3,2,3,4,5,5,4,3,4,5,6,6,5,4,…,则第2016个数是( )
| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
18.设集合M={x|0≤x<1},集合N={x|x2-2x-3≥0},则集合M∩(∁RN)=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
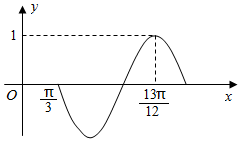 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.