题目内容
15.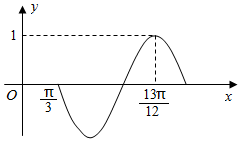 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(Ⅰ)写出函数f(x)的最小正周期T及ω、φ的值;
(Ⅱ)求函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最大值与最小值.
分析 (I)由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(II)由以上可得,f(x)=sin(2x+$\frac{π}{3}$),再利用正弦函数的定义域和值域,求得函数的最值.
解答 解:(I)根据函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象,
可得$\frac{3}{4}•\frac{2π}{ω}$=$\frac{13π}{12}$-$\frac{π}{3}$,求得ω=2,∴最小正周期T=$\frac{2π}{2}$=π.
再根据五点法作图可得2•$\frac{π}{3}$+φ=π,求得φ=$\frac{π}{3}$.
(II)由以上可得,f(x)=sin(2x+$\frac{π}{3}$),在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上,
2x+$\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],sin(2x+$\frac{π}{3}$)∈[-$\frac{1}{2}$,1],
当2x+$\frac{π}{3}$=-$\frac{π}{6}$时,即x=-$\frac{π}{4}$,函数f(x)取得最小值为-$\frac{1}{2}$.
当2x+$\frac{π}{3}$=$\frac{π}{2}$时,即x=$\frac{π}{12}$,函数f(x)取得最大值为1.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,正弦函数的最值,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
7.已知(1+i)i=a+bi(a,b∈R),其中i为虚数单位,则a+b的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
4.命题“?x∈R,x2是无理数”的否定是( )
| A. | ?x∉R,x2不是无理数 | B. | ?x∈R,x2不是无理数 | ||
| C. | ?x∉R,x2不是无理数 | D. | ?x∈R,x2不是无理数 |
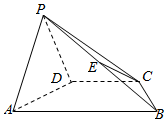 如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.
如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.