题目内容
17.如图,在菱形ABCD中,AB=2,∠DAB=60°,E为CD的中点,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的值是( )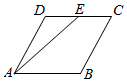
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
分析 将$\overrightarrow{AE}$表示为$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,代入$\overrightarrow{AD}$•$\overrightarrow{AE}$,展开后利用向量数量积运算得答案.
解答 解:∵E为CD的中点,
∴$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,
又ABCD为菱形,且AB=2,∠DAB=60°,
∴$\overrightarrow{AD}$•$\overrightarrow{AE}$=$\overrightarrow{AD}•(\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB})$=$|\overrightarrow{AD}{|}^{2}+\frac{1}{2}\overrightarrow{AD}•\overrightarrow{AB}$
=$|\overrightarrow{AD}{|}^{2}+\frac{1}{2}|\overrightarrow{AD}|•|\overrightarrow{AB}|cos60°$=$4+\frac{1}{2}×2×2×\frac{1}{2}=5$.
故选:B.
点评 本题考查向量的数量积运算,考查向量的加减法则,是中档题.

练习册系列答案
相关题目
2.设集合M={x|(x-3)(x+2)<0},N={x|x-1>0},则M∩N=( )
| A. | (1,2) | B. | (1,3) | C. | (-1,2) | D. | (-1,3) |
7.已知(1+i)i=a+bi(a,b∈R),其中i为虚数单位,则a+b的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |