题目内容
数列{an}满足an=
(k∈N*),设f(n)=a1+a2+…+a2n-1+a2n,则f(2014)-f(2013)等于 .
|
考点:数列的求和,数列的概念及简单表示法
专题:等差数列与等比数列
分析:根据题意可看出数列奇数项的和a1+a3+…+a2n-1=
=4n-1,偶数项的和a2+a4+…+a2n=a1+a2+…+a2n-1=f(n-1).从而可以表示出f(n)=4n-1+f(n-1),所以f(2014)-f(2013)=42013.
| 2n-1(2n-1+1) |
| 2 |
解答:
解:∵an=
(k∈N*),
f(n)=a1+a2+…+a2n-1+a2n,
∴数列前2n项中奇数项的和,
a1+a3+…+a2n-1=
=4n-1,
数列前2n项中偶数项的和,
a2+a4+…+a2n=a1+a2+…+a2n-1
=f(n-1).
∴f(n)=4n-1+f(n-1),
∴f(2014)-f(2013)=42013.
故答案为:42013
|
f(n)=a1+a2+…+a2n-1+a2n,
∴数列前2n项中奇数项的和,
a1+a3+…+a2n-1=
| 2n-1(2n-1+1) |
| 2 |
数列前2n项中偶数项的和,
a2+a4+…+a2n=a1+a2+…+a2n-1
=f(n-1).
∴f(n)=4n-1+f(n-1),
∴f(2014)-f(2013)=42013.
故答案为:42013
点评:本题主要考查数列递推式的灵活应用,幂运算的简单应用等,属于难题.解题的关键是表示出f(n).

练习册系列答案
相关题目
已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上单调递减,设a=f(0),b=f(2),c=f(-1),则( )
| A、a<c<b |
| B、a<b<c |
| C、b<c<a |
| D、c<b<a |
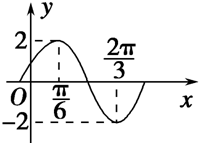
如图已知函数y=Asin(ωx+φ)的部分图象,则表达式为( )

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(2x-
|