题目内容
8.设[x]表示不超过x的最大整数,如[4.3]=4,[-4,3]=-5.化简:$\frac{1}{[\sqrt{1×2}]×[\sqrt{2×3}]×[\sqrt{3×4}]}$+$\frac{1}{[\sqrt{2×3}]×[\sqrt{3×4}]×[\sqrt{4×5}]}$+…+$\frac{1}{[\sqrt{n×(n+1)}]×[\sqrt{(n+1)×(n+2)}]×[\sqrt{(n+2)×(n+3)}]}$(结果用n表示,其中n是大于0的整数).分析 利用设[x]表示不超过x的最大整数,依次化简个根式,然后利用裂项相消法即可得结论.
解答 解:由题意,[x]表示不超过x的最大整数,设n为正整数,则$n<\sqrt{n({n+1})}<n+1$,于是,$[{\sqrt{n({n+1})}}]=n$,
∴$\frac{1}{{[\sqrt{n×(n+1)}]×[\sqrt{(n+1)×(n+2)}]×[\sqrt{(n+2)×(n+3)}]}}=\frac{1}{n×(n+1)×(n+2)}=\frac{1}{2}(\frac{1}{n×(n+1)}-\frac{1}{(n+1)×(n+2)})$,
∴原式=$\frac{1}{2}(\frac{1}{1×2}-\frac{1}{2×3}+\frac{1}{2×3}-\frac{1}{3×4}+…+\frac{1}{n×(n+1)}-\frac{1}{(n+1)×(n+2)})$
=$\frac{1}{4}-\frac{1}{2(n+1)×(n+2)}$.
点评 本题考查了对定义的理解和裂项相消法的计算.属于中档题.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
18.曲线y=eaxcosx在x=0处的切线与直线x+2y=0垂直,则a=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.如果二次方程x2-px-q=0(其中p,q均是大于0的整数)的正根小于3,那么这样的二次方程有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,过F2的直线与椭圆交于A、B两点,若△F1AB是等边三角形,则离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{3}{4}$ |
10.函数f(x),x∈R满足如下性质:①f(x)+f(-x)=0;②f($\frac{3}{4}$+x)=f($\frac{3}{4}$-x),若f(1)=-$\frac{\sqrt{5}}{5}$,f(2)=sinα(α∈(0,$\frac{π}{2}$)),则sin($\frac{π}{4}$+α)=( )
| A. | 0 | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
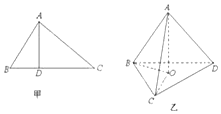 如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.
如图甲,在△ABC中,AB⊥AC,AD⊥BC,D为.垂足,则AB2=BD•BC,该结论称为射影定理.如图乙,在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,探究S△ABC、S△BCO、S△BCD这三者之间满足的关是S△ABC2=S△BCO•S△BCD.