题目内容
8.已知函数$f(x)={log_2}(x+\sqrt{{x^2}+1})+\frac{{5{e^x}+3}}{{{e^x}+1}}$,x∈[-k,k](k>0)的最大值和最小值分别为M和m,则M+m=8.分析 由函数f(x)变形,构造函数g(x)=log2(x+$\sqrt{1+{x}^{2}}$)+$\frac{{e}^{x}-1}{{e}^{x}+1}$,x∈[-k,k](k>0),判断它为奇函数,设出最大值和最小值,计算即可得到所求最值之和.
解答 解:函数$f(x)={log_2}(x+\sqrt{{x^2}+1})+\frac{{5{e^x}+3}}{{{e^x}+1}}$
=log2(x+$\sqrt{1+{x}^{2}}$)+5-$\frac{2}{1+{e}^{x}}$
=log2(x+$\sqrt{1+{x}^{2}}$)+$\frac{{e}^{x}-1}{{e}^{x}+1}$+4,
构造函数g(x)=log2(x+$\sqrt{1+{x}^{2}}$)+$\frac{{e}^{x}-1}{{e}^{x}+1}$,x∈[-k,k](k>0),
即有g(-x)+g(x)=log2(-x+$\sqrt{1+{x}^{2}}$)+$\frac{{e}^{-x}-1}{{e}^{-x}+1}$+log2(x+$\sqrt{1+{x}^{2}}$)+$\frac{{e}^{x}-1}{{e}^{x}+1}$
=log2(1+x2-x2)+$\frac{1-{e}^{x}}{1+{e}^{x}}$+$\frac{{e}^{x}-1}{{e}^{x}+1}$=0,
即g(x)为奇函数,
设g(x)的最大值为t,则最小值即为-t,
则f(x)的最大值为M=t+4,最小值为m=-t+4,
即有M+m=8.
故答案为:8.
点评 本题考查函数的最值的求法,注意运用构造函数,判断奇偶性,考查运算能力,属于中档题.

练习册系列答案
相关题目
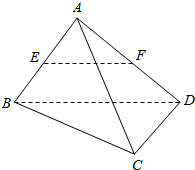 在空间四边形ABCD中,E,F分别是AB,AD的中点
在空间四边形ABCD中,E,F分别是AB,AD的中点