题目内容
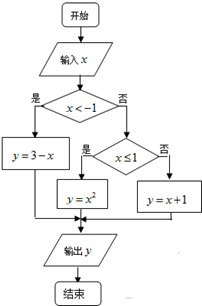 阅读右边的算法流程图(如图),解答下列问题:
阅读右边的算法流程图(如图),解答下列问题:(1)写出算法输出的结果y=f(x);
(2)已知命题p:{x|f(x)≤1};命题q:关于x的不等式x2-3ax+2a2>0(a>0)的解集,且q是p的必要不充分条件,求a的取值范围.
考点:程序框图
专题:集合,算法和程序框图,简易逻辑
分析:(1)由已知中的程序框图可得:该程序的功能是计算并输出分段函数:f(x)=
的函数值;
(2)解f(x)≤1可得P,解不等式x2-3ax+2a2>0(a>0)可得Q,进而根据q是p的必要不充分条件,可得[-1,1]?(-∞,a)∪(2a,+∞),进而得到答案.
|
(2)解f(x)≤1可得P,解不等式x2-3ax+2a2>0(a>0)可得Q,进而根据q是p的必要不充分条件,可得[-1,1]?(-∞,a)∪(2a,+∞),进而得到答案.
解答:
解:(1)由已知中的程序框图可得:
该程序的功能是计算并输出分段函数:f(x)=
的函数值;
(2)当x<-1时,由3-x≤1得,x≥2,故不存在满足条件的x值;
当-1≤x≤1时,由x2≤1得,-1≤x≤1,故-1≤x≤1;
当x>1时,由x+1≤1得,x≤0,故不存在满足条件的x值;
综上:{x|f(x)≤1}=[-1,1];
解不等式x2-3ax+2a2>0(a>0)可得:x∈(-∞,a)∪(2a,+∞),
∵q是p的必要不充分条件,
∴[-1,1]?(-∞,a)∪(2a,+∞),
故a>1.
该程序的功能是计算并输出分段函数:f(x)=
|
(2)当x<-1时,由3-x≤1得,x≥2,故不存在满足条件的x值;
当-1≤x≤1时,由x2≤1得,-1≤x≤1,故-1≤x≤1;
当x>1时,由x+1≤1得,x≤0,故不存在满足条件的x值;
综上:{x|f(x)≤1}=[-1,1];
解不等式x2-3ax+2a2>0(a>0)可得:x∈(-∞,a)∪(2a,+∞),
∵q是p的必要不充分条件,
∴[-1,1]?(-∞,a)∪(2a,+∞),
故a>1.
点评:本题考查的知识点是程序框图,二次不等式的解法,分段函数,充要条件,集合的包含关系,是函数、不等式、算法、集合的简单综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知|
|=|
|=1向量
与
的夹角为120°,且(
+
)⊥(
+t
),则实数t的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、-1 | B、1 | C、-2 | D、2 |
下列与抛物线y=
x2具有公共焦点的双曲线( )
| 1 |
| 8 |
| A、A、16y2-32x2=1 | ||||
B、
| ||||
C、
| ||||
D、x2-
|
当向量
=c=(-2,2),
=(1,0)时,执行如图所示的程序框图,输出的i值为( )
| a |
| b |

| A、5 | B、4 | C、3 | D、2 |
若
=(-5,4),
=(7,9),向量
同向的单位向量坐标是( )
| OA |
| OB |
| AB |
A、( -
| ||||
B、(
| ||||
C、( -
| ||||
D、(
|
 执行如图所示的程序框图,如果输入-2,那么输出的结果是
执行如图所示的程序框图,如果输入-2,那么输出的结果是