题目内容
已知二项式(x+
)n(n∈N*,n≥2).
(1)若该二项式的展开式中前三项的系数成等差数列,求正整数n的值;
(2)在(1)的条件下,求展开式中x4项的系数.
| 1 |
| 2x |
(1)若该二项式的展开式中前三项的系数成等差数列,求正整数n的值;
(2)在(1)的条件下,求展开式中x4项的系数.
考点:二项式定理的应用
专题:二项式定理
分析:(1)利用二项展开式的通项公式求出展开式的前3项,利用等差数列,得到关系式,即可求出n的值.
(2)利用通项,令x的指数为4,求出r,然后求出所求结果.
(2)利用通项,令x的指数为4,求出r,然后求出所求结果.
解答:
解:(1)由题知2×(
)=
+(
)2
,…(2分)
故n2-9n+8=0,
从而n=1或n=8
由于n≥2,故n=8…(4分)
(2)由上知其通项公式为
x8-r(
)r,即
(
)rx8-2r…(6分)
令8-2r=4得r=2…(8分)
故x4项的系数为
(
)2=7.…(10分)
| 1 |
| 2 |
| C | 1 n |
| C | 0 n |
| 1 |
| 2 |
| C | 2 n |
故n2-9n+8=0,
从而n=1或n=8
由于n≥2,故n=8…(4分)
(2)由上知其通项公式为
| C | r 8 |
| 1 |
| 2x |
| C | r 8 |
| 1 |
| 2 |
令8-2r=4得r=2…(8分)
故x4项的系数为
| C | 2 8 |
| 1 |
| 2 |
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知复数z满足(1+i)
=3+i,z等于( )
. |
| z |
| A、2+i | B、2-i |
| C、-2-i | D、-2+i |
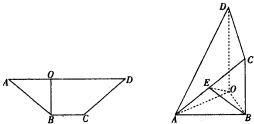 在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.
在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点. 某高三7班30名男生1000米跑统测成绩的茎叶图(如果某学生1000米测试成绩是x分y秒,x为茎,y为叶)如图.
某高三7班30名男生1000米跑统测成绩的茎叶图(如果某学生1000米测试成绩是x分y秒,x为茎,y为叶)如图.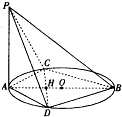 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面