题目内容
已知椭圆
+
=1的左焦点在抛物线C:y2=2px(p>0)的准线上,F为抛物线的焦点.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若直线l过点F交抛物线于不同的两点A、B,交y轴于点M,且
=a
,
=b
,则对任意的直线l,a+b是否为定值?若是,求出a+b的值;否则,请说明理由.
| x2 |
| p2 |
| y2 |
| 3 |
(Ⅰ)求抛物线C的方程;
(Ⅱ)若直线l过点F交抛物线于不同的两点A、B,交y轴于点M,且
| MA |
| AF |
| MB |
| BF |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆
+
=1的左焦点为(-
,0),抛物线C:y2=2px(p>0)的准线x=-
,建立方程,可求p的值,从而可得抛物线C的方程;
(Ⅱ)设直线l:y=k(x-1),l与y轴交于M(0,-k),设直线l交抛物线于A(x1,y1),B(x2,y2),与抛物线联立,消元利用韦达定理,结
=a
,
=b
,可得a,b,由此可得结论.
| x2 |
| p2 |
| y2 |
| 3 |
| p2-3 |
| p |
| 2 |
(Ⅱ)设直线l:y=k(x-1),l与y轴交于M(0,-k),设直线l交抛物线于A(x1,y1),B(x2,y2),与抛物线联立,消元利用韦达定理,结
| MA |
| AF |
| MB |
| BF |
解答:
解:(Ⅰ)椭圆
+
=1的左焦点为(-
,0),抛物线C:y2=2px(p>0)的准线x=-
,
∴-
=-
,
∴p=2,
∴抛物线C的方程为y2=4x;
(Ⅱ)由已知得直线l的斜率一定存在,所以设l:y=k(x-1),l与y轴交于M(0,-k),
设直线l交抛物线于A(x1,y1),B(x2,y2),
直线l代入抛物线方程,可得k2x2-(2k2+4)x+k2=0
∴x1+x2=2+
,x1x2=1
∵
=a
,∴(x1,y1+k)=(1-x1,-y1),∴a=
,
同理b=
,
∴a+b=
+
=-1,
∴对任意的直线l,a+b为定值-1.
| x2 |
| p2 |
| y2 |
| 3 |
| p2-3 |
| p |
| 2 |
∴-
| p2-3 |
| p |
| 2 |
∴p=2,
∴抛物线C的方程为y2=4x;
(Ⅱ)由已知得直线l的斜率一定存在,所以设l:y=k(x-1),l与y轴交于M(0,-k),
设直线l交抛物线于A(x1,y1),B(x2,y2),
直线l代入抛物线方程,可得k2x2-(2k2+4)x+k2=0
∴x1+x2=2+
| 4 |
| k2 |
∵
| MA |
| AF |
| x1 |
| 1-x1 |
同理b=
| x2 |
| 1-x2 |
∴a+b=
| x1 |
| 1-x1 |
| x2 |
| 1-x2 |
∴对任意的直线l,a+b为定值-1.
点评:本题考查抛物线方程,考查直线与抛物线的位置关系,考查向量知识的运用,联立方程,利用韦达定理是关键.

练习册系列答案
相关题目
点P与定点F(8,0)的距离和它到定直线x=2的距离的比是2,则点P的轨迹方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
A、向量
| ||||
| B、两个有共同起点长度相等的向量,则终点相同 | ||||
| C、零向量没有方向 | ||||
| D、任一向量与零向量平行 |
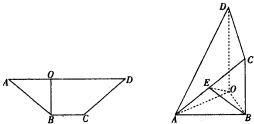 在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.
在等腰梯形ABCD中,BC∥AD,BO⊥AD于O,且AD=3BC=3BO,现将梯形沿BO折叠,使得△AOB所在平面与四边形OBCD所在平面互相垂直,连接AD、AC,E是AC中点.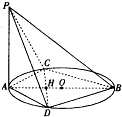 已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面
已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面