题目内容
证明函数f（x）=x6-x3+x2-x+1的值恒为正数．
考点：利用导数求闭区间上函数的最值
专题：推理和证明
分析：可对x的所有不同取值逐一给出证明，即完全归纳推理．
解答：
证明：当x＜0时，f（x）各项都是正数，
∴当x＜0时，f（x）为正数，
当0≤x≤1时，f（x）=x6+x2（1-x）+（1-x）＞0；
当x＞1时，f（x）=x3（x3-1）+x（x-1）+1＞0．
综上所述，f（x）的值恒为正数．
∴当x＜0时，f（x）为正数，
当0≤x≤1时，f（x）=x6+x2（1-x）+（1-x）＞0；
当x＞1时，f（x）=x3（x3-1）+x（x-1）+1＞0．
综上所述，f（x）的值恒为正数．
点评：本题主要考查了函数的最值的问题，采用分类讨论的思想，以及完全归纳推理的问题，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=xlnx的（ ）
A、极小值为
| ||
B、极大值为
| ||
C、极小值为-
| ||
D、极大值为-
|
若幂函数f（x）=xm-1在（0，+∞）上是减函数，则（ ）
| A、m＞1 | B、不能确定 |
| C、m=l | D、m＜1 |
下列说法正确的是（ ）
A、向量
| ||||
| B、两个有共同起点长度相等的向量，则终点相同 | ||||
| C、零向量没有方向 | ||||
| D、任一向量与零向量平行 |
已知O，T，P在△ABC所在平面内，且
+
+
=
，|
|=|
|=|
|，且
•
=
•
=
•
，则点O，T，P依次是△ABC的（ ）
| OA |
| OB |
| OC |
| 0 |
| TA |
| TB |
| TC |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| A、外心 重心 垂心 |
| B、重心 外心 内心 |
| C、重心 外心 垂心 |
| D、外心 重心 内心 |
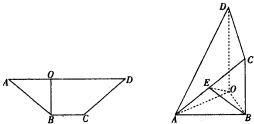在等腰梯形ABCD中，BC∥AD，BO⊥AD于O，且AD=3BC=3BO，现将梯形沿BO折叠，使得△AOB所在平面与四边形OBCD所在平面互相垂直，连接AD、AC，E是AC中点．