题目内容
已知点P为圆x2+y2=1上的动点,点Q的坐标为(4,0).
(1)求PQ的中点M的轨迹方程;
(2)若△PQA为正三角形,求点A的轨迹方程.
(1)求PQ的中点M的轨迹方程;
(2)若△PQA为正三角形,求点A的轨迹方程.
考点:轨迹方程
专题:综合题,直线与圆
分析:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程即得线段PQ中点的轨迹方程.
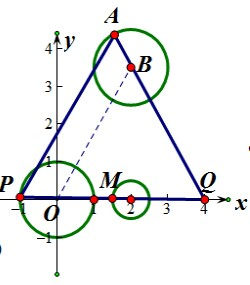
(2)A与P轨迹形状是相同的,只是圆心位置不同,如图,B为圆心.求出B的坐标,即可求点A的轨迹方程.
(2)A与P轨迹形状是相同的,只是圆心位置不同,如图,B为圆心.求出B的坐标,即可求点A的轨迹方程.
解答:
 解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=
解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=
.
(2)∵Q为定点,
∴A与P轨迹形状是相同的,只是圆心位置不同,如图,B为圆心.
当P在(-1,0)时,可知AP∥BO,
则直线BO:y=
x,直线BQ:y=-
(x-4),
联立方程可得B(2,2
),
∴点A的轨迹方程是(x-2)2+(y-2
)2=1
 解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=
解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=| 1 |
| 4 |
(2)∵Q为定点,
∴A与P轨迹形状是相同的,只是圆心位置不同,如图,B为圆心.
当P在(-1,0)时,可知AP∥BO,
则直线BO:y=
| 3 |
| 3 |
联立方程可得B(2,2
| 3 |
∴点A的轨迹方程是(x-2)2+(y-2
| 3 |
点评:求曲线的轨迹方程常采用的方法有直接法、定义法、相关点代入法、参数法,本题主要是利用直接法和相关点代入法,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.相关点代入法 根据相关点所满足的方程,通过转换而求动点的轨迹方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=
,则f(x)在x=
处切线的斜率为( )
| cos2x |
| x |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|

 g′(x)是函数g(x)=sin2(2x+
g′(x)是函数g(x)=sin2(2x+